青井研究室
担当教員/青井 久
3次元の世界で生活している私達にとって、「4次元」の世界は未知なる領域だと思われるかもしれません。しかしながら、数学ではごく普通に考えられ、議論が展開されています。それどころか、5次元、6次元などという世界も当たり前のように出てきます。
私が興味をもっているのは、これら「有限次元」の先にある、「無限次元」の世界です。そこでは、有限では考えられない現象が起こっています。「作用素環論」の対象は、この不思議な世界に「作用している」ものです。「解析学」として分類されていますが、代数学、幾何学とも密接に関わっています。我々の現実世界においても、量子力学や結び目理論などが関連しています。
数学の中では比較的新しいこの分野、未知の問題も数多くありますが、それだけやりがいのある研究対象だと考えています。
数理ファイナンス研究室
担当教員/赤堀 次郎・天羽 隆史・今村 悠里
当研究室では確率論および数理ファイナンスの広範にわたる分野を研究しています。例年、学部学生30〜40名(学科全体の1/3〜1/2)が当研究室に所属、大学院生もコハツ研と併せて10〜20名(学科全体の80%以上)が所属している、大所帯です。世界中からゲストが頻繁に訪れて共同研究をおこなっています。構成員が多いため、研究テーマは多岐にわたっていますが、その中の一部を挙げると「エキゾチックオプションの価格付け」「金利の期間構造の統計分析」「ゼータ関数の確率論的表示」「確率微分方程式の微分幾何学的研究」などです。

セミナー風景
石井研究室
担当教員/石井 秀則
本研究室では整数論、とりわけ、保型形式に付随するL関数の研究が最終目的となっています。保型形式に付随するL関数は、現在知られているL関数の中で最も重要なものの1つです。世の中には様々なL関数が知られていますが、新しいL関数を発見することや、L関数たちの間の関係を見つけることが整数論の究極の目的であると言っても過言ではありません。1994年に、Wilesは360年間未解決だったフェルマー予想を証明しましたが、その本質は、有理数体上の楕円曲線のL関数は保型形式に付随するL関数であるという志村・谷山予想の解決にありました。また、整数論は現代の高度情報ネットワーク社会では欠くことができない暗号技術・認証技術へ重要な応用を持っています。合わせて、ネットワークに関するアルゴリズムの数学的基礎研究もおこなっています。

セミナー風景
大坂研究室
担当教員/大坂 博幸
数学モデルを抽象化しその本質を探る関数解析学が研究室の看板ですが、最近は、数理物理学、組紐理論、位相幾何学、偏微分方程式、確率論など様々な卒研が実施されています。また、中学・高校教育の教材に繋がる卒研に取り組んだりしています。
「無限次元線形代数学」といわれます作用素環論が研究対象です。個々の現象を表す関数を調べる代わりに、その関数の束からなる関数空間を考えるという思想でバナッハ空間論が展開されますが、それに代数構造を入れることで、発生するC*-環の分類問題に取り組んでいます。最近は、経済理論に応用がある単調増加関数に付随する問題に取り組み、高校生に馴染みのある相加平均・相乗平均の一般化であるイエセンの不等式に関する新しい結果を出しています。また、暗号理論に応用があると期待されている量子情報理論の研究にも取り組みはじめています。
とおくと、相加平均・相乗平均の関係式が導ける。
計算してみよう!!
加川研究室
担当教員/加川 貴章
私の専門は整数論、特に実二次体上の楕円曲線の分類を、ここ数年面白がってやっています。そもそも整数論をやるようになったきっかけの一つが、大学(早稲田)時代の指導教官の足立恒雄先生が書かれた「フェルマーの大定理」という本でしたし、楕円曲線をいじるようになったきっかけの一つが、フェルマーの大定理の解決に楕円曲線の理論が使われたことでした。整数論は具体的なことが魅力の一つです。二次体、楕円曲線は、具体的で触りやすいのに、未解決なことがたくさんあります。どんどん解決していきたいので、学生さんがよき協力者になってくれることを願っています。
コハツ研究室
担当教員/KOHATSU-HIGA ARTURO・田中 秀幸・中津 智則
数学の観点からみたさまざまなシミュレーション方法についての研究を行っています。
現在は、特にファイナンスの問題に応用可能なシミュレーション方法についての研究を行っています。
近年の金融機関ではさまざまなリスクを計るために、気象現象のように複雑な事象に関してのシミュレーションを繰り返していて、しかもそれを瞬時に行う必要があります。このためには、高度な数学理論を用いたシミュレーションそのもの、より高度な理論が必要だということが現在広く認識されています。私たちのグループも、純粋数学を基本としながらも、確率、統計の具体的計算やその計算のためのプログラミングを非常に大事な要素として日々研究を行っています。

高山研究室
担当教員/高山 幸秀
多項式の連立方程式の解集合を、代数学、幾何学、解析学の方法を使って研究するのが代数幾何学です。日本は3人のフィールズ賞受賞者をはじめ、世界的指導者を数多く輩出しており、代数幾何学はいわば日本のお家芸として現在でも活発に研究されています。その中で私は正標数の代数幾何学という、素数に関係する分野に興味を持っています。正標数の世界では、標数零の世界で大活躍するコホモロジーの消滅定理は一般には成り立ちませんし、標数零では可能な特異点解消もできるかどうかよくわかっていません。このように標数零の世界とは異なる不思議な現象が数多く見られ、それらに潜む数学的原理の探求は興味深い研究テーマです。現在、標数零で開発されたさまざまな方法や可換環論の分野で開発された方法を使って、この問題に取り組んでいます。

ゼミで使うテキスト。高度な代数学の理論を駆使して、高次元の幾何学を研究する。
辻下研究室
担当教員/辻下 徹
数学は一世紀前に「無限の逆理」を取り込み、終わることのないプロセスを終わったものとして扱うことにして爆発的に発展しましたが、その副作用として有限概念が一種類に退化し有限世界にある質的多様性を捉える数学的枠組があまり発展しませんでした。21世紀の数学は「砂山の逆理」を取り込み複数の有限概念を土台として有限世界をとらえる豊かな概念体系を産みだすことにより「複雑システム学」のための数学的基盤を形成することを予想しています。
卒研生は21世紀数学で活性化することが予想される原生的数学の一端に「具象数学」と「実験数学」を通して触れ、大学院生は複数の有限概念を土台とする数学の建設に参加します。
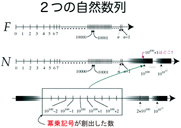
十進法による数列 F とべき記号も使う数列 N の「長さの違い」を質的にとらえる数学を模索。
野澤研究室
担当教員/野澤 啓
川は水の流線の集まりとみなすことができます。葉層構造とは、そのような状況をより一般の空間において抽象化したものです。つまり、葉層構造とはある空間(例えば3次元の川)のより小さい次元の空間(例えば1次元の水の流線)への分割のことです。葉層構造は微分方程式や2次元の空間上の力学系との関連から50年ほど前に現代的な研究が行われ始め、その後、3次元多様体論、群作用の理論、微分幾何などの分野と関わりながら発展してきました。私はコホモロジーや特性類と呼ばれる位相幾何の道具を用いて、葉層構造の大域的性質を研究しています。近年の研究の主な目標はリーマン多様体の測地流の安定葉層や等質空間上の葉層構造の「剛性」と呼ばれる不思議な性質を解明することです。

ドーナツ状の空間の上のReeb葉層の切断面
福本研究室
担当教員/福本 善洋
宇宙はどのような形をしているのでしょうか?私たちの知覚では、縦と横と高さの3つの広がりを持っているように感じます。この広がりはどこまでもつづくのでしょうか?それとも、ずっと進むうちにどこか遠くでつながっていて、また戻ってくるようなことがあるのでしょうか。それは時間とともに形を変えて行くのでしょうか。だとすれば、どのように形を変えていくのでしょうか。
このような広がりをもった「空間」を理解し、さらにその「空間」が時間とともに発展していく様子を「トポロジー」という幾何学の一分野を使って研究しています。そして、インスタントンやモノポールといった粒子(場)の振る舞いを調べる「ゲージ理論」という物理の方法を使うことで、この研究の可能性を深めていきます。
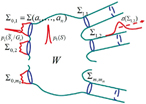
ゲージ理論のトポロジーへの応用
藤家研究室
担当教員/藤家 雪朗
高校の物理で習うように、惑星やボールの運動はニュートンの運動方程式で記述されます。これは時間を変数とする常微分方程式です。一方、電子や原子核のような微視的な物体の運動を記述するのは、シュレディンガー方程式という、時間と空間に関する微分を含んだ偏微分方程式です。ニュートンの運動方程式を基礎にした古典力学は、シュレディンガー方程式に含まれるプランク定数が0に近づいたときの極限(準古典極限)として捉えることができると、物理学者のボーアは提唱しています。
この仮説は数学において準古典解析という一つの厳密な理論として、近年著しく発展しています。微分方程式はごく限られた特別な場合を除いて、具体的に解を求めることはできません。しかし準古典極限で解がどのような漸近的な振る舞いをするかは具体的にわかることが多く、したがってシュレディンガー作用素の固有値や散乱振幅など、様々な物理量の漸近展開が求められます。この漸近展開の各項に一体どのような古典力学の量が現れるのか、計算を通して新しい発見をする楽しみがこの分野にはあります。
安富研究室
担当教員/安富 健児
近代的な確率論を学びます。
取り得る“状態”が有限の場合(硬貨投げの表裏、サイコロの出目等)の場合は素朴に一つ一つの“状態”の確率を考える事ができますが、取り得る“状態”が非可算無限の場合は有限の時と同じように一つの“状態”に確率を考えるとその確率の値をどの様においたとしても矛盾を生じます。
近代的な確率論は、大きさを測るという概念の抽象化により、その様なジレンマを解決し、非可算無限個の“状態”を持つ確率を考える事を可能にします。一方でこの抽象化は大きさを測れない集合の存在という新たなジレンマを生みます。
この様に確率論はそれ自体が興味深い対象です。また一方では統計的な手法と結びつく事により実社会の様々な局面で実際に応用されているという側面を併せ持つという面白い数学の分野です。

黒板/数学は黒板とチョーク又は紙と鉛筆があれば何処でもできます
渡部研究室
担当教員/渡部 拓也
微分方程式で記述される古典力学や、微分作用素のスペクトル(固有値)で記述される量子力学、それらの背景にある数学的構造が研究のテーマです。典型的な現象を記述する微分方程式は数学的に美しい構造をもつため、その解析は大学で学ぶ様々な解析手法(線形代数・複素解析・関数解析・フーリエ解析)が見事に活躍する分野です。卒業研究では、学生自身の興味に沿って手法を絞って微分方程式の解析理論を学んでいます。私自身は、小さなパラメータ(特異摂動)を含んだ微分方程式の解析に取り組んでいます。この研究分野は、量子力学と古典力学を関係づけることから準古典解析と呼ばれます。キーワードはストークス現象と呼ばれるものですが、これは複素数の世界に目を向けて初めて見えるもので、数学的に興味深い問題です。

虹の内側に過剰虹と呼ばれるものが見えることがあります。
これはエアリーの微分方程式のストークス現象によって説明されます。












