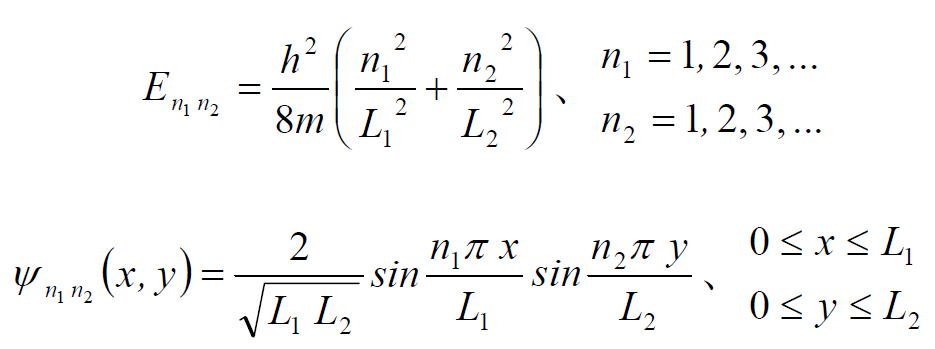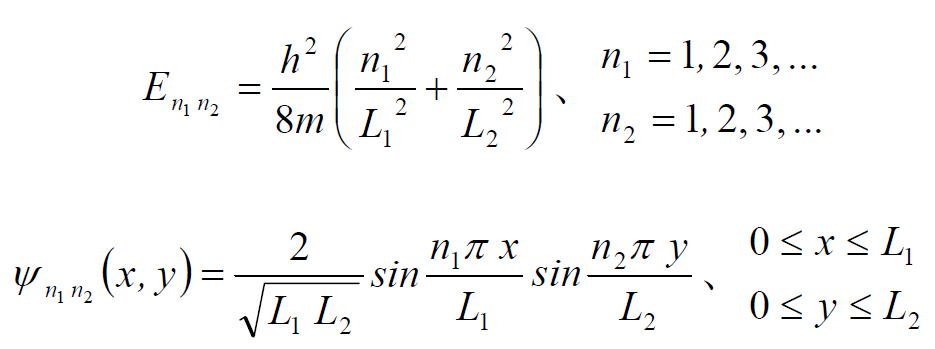Mathematicaには色々な3次元プロットの機能がついている。
その細かい機能設定についてはヘルプを参照。

課題１　表面プロット

1. 10sin(x + siny)を、-10<x<10, -10<y<10の範囲で、表面プロットしてみる。Plot3D[関数, {xの範囲}, {yの範囲}]を使う。
2. z軸の範囲（PlotRange->{範囲}）を、-5<z<5にしてみる。
   解像度が足りない場合は、「PlotPoints->点数」で解像度を上げることもできる。
3. 等高線プロットContourPlot[f, {x, min, max}, {y, min, max}]してみる。

練習２
無限に深い２次元の井戸型ポテンシャル中の粒子のエネルギーと波動関数は、つぎのように表される。

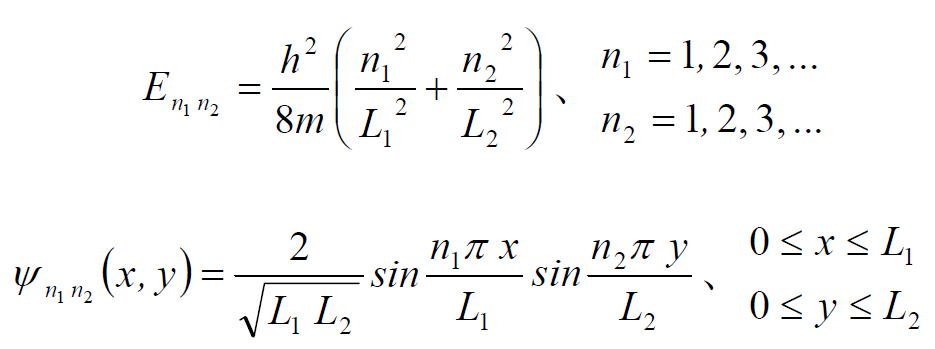
ここで L₁とL₂は井戸の幅である。
井戸の外の世界は存在しないので、井戸の中だけ表示すればいい。
等高線プロットにはContourPlot[f, {x, min, max}, {y, min, max}]を使う。
アスペクト比は、AspectRatio→L₂/L₁と定義する。

1. 変数がたくさんあって面倒なので、独自関数を定義する。
   hako[n1_, n2_, L1_, L2_] = ContourPlot[f, {x, min, max}, {y, min, max}, AspectRatio→L₂/L₁]
   のような形式になる。独自関数に使う変数を定義する場合は、「_」（アンダーバー）をつけることを忘れずに。
2. L₁ =2, L₂ = 1、n₁ = 3, n₂ = 2 として、この波動関数を等高線プロットで表してみよう。
   hako[3, 2, 2, 1]と、変数の値を独自関数に代入。
3. L₁とL₂ がどのようなときに「縮退」が起きるか考え、互いに縮退している状態の波動関数を、等高線プロットで描け。

課題３
3次元プロット。ParametricPlot3D[{f_x(u, v), f_y(u, v), f_z(u, v)}, {uの範囲, vの範囲}]を使う。

1. 円柱を描く。
2. 円錐を描く。
3. 螺旋を描く。
4. 球を描く。
5. 楕円球を描く。
6. トーラスを描く。
7. 円柱とトーラスを合わせて描く。

課題４
多面体を描こう。

1. PolyhedronData[ ]を使って テトラヘドロン、ヘキサヘドロン、オクタヘドロン、ドデカヘドロン、イコサヘドロンなどを描こう。
2. 二つ以上の多面体を１つの図に描いてみよう。Show[関数1, 関数2, …]を使う。

課題提出方法：

• メールのタイトルは”基礎演習２レポート：氏名と学生証番号”とすること。
• 提出ファイルの先頭のinputに、必ず氏名と学生証番号を記入すること。
• ファイル名は “氏名+151128.nb”とする。
  （例：立命太郎151128.nb）
• ファイル名の「氏名」以外は必ず半角。
• 最終締め切り：2015年12月4日（金曜）。
• 日常点評価の提出課題は定期試験と同等の意味があるので真剣に取り組むこと。