今日は、Mathematicaを使って量子力学の勉強をする。

課題１　無限に深い箱の中の粒子
x = 0とx = Lに無限に高いポテンシャルの壁があり、 0 < x < Lの範囲ではポテンシャルがゼロの場合、その中に閉じ込められた素粒子のエネルギーE_nと波動関数は以下のように表される。ここでmは粒子の質量、hはプランク定数である。

　ただし、n = 1, 2, 3, 4, …

n = 1, 2, 3, 4のときの波動関数をPlot[　]を使って描いてみよう。ただし、L = 1とする。

課題２　箱形ポテンシャルの2次元への拡張
無限に深い２次元の箱型ポテンシャル中の粒子のエネルギーと波動関数は、つぎのように表される。

ここで L₁とL₂は井戸の幅である。簡単のためL₁ = L₂ = 1 として、この波動関数を３次元プロットと等高線プロットの両方で表してみよう。
a) Plot3D[f[x, y], {x, min, max}, {y, min, max}, AspectRatio -> 1]を使って、３次元プロットする。
b) 等高線プロットにはContourPlot[f[x, y], {x, min, max}, {y, min, max}, AspectRatio -> 1]を使う。
c) 縮退した状態を描いてみよう。

課題３　中心力により球面上を運動する量子力学的粒子の球面調和関数Y_l,ml (θ,φ)を図示してみよう。
そのエネルギーはつぎのように表される
　

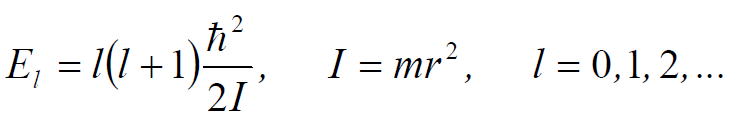
ここで、I は慣性モーメントであり、l は方位量子数、m_lは磁気量子数である。
l = 0, 1, 2, 3, ...であるのに対し、m_l = -l , -l +1, ..., 0, ... ,l -1, l である。

エネルギー状態は方位量子数l のみに依存し、磁気量子数m_lには依存しないので、波動関数は（2l + 1）重に縮退している。
このような波動関数を球面調和関数Y_l,ml (θ,φ)と呼ぶ。

Y_l,ml (θ,φ)の形状についてはアトキンスの物理化学（上）p. 358 の表12.3 などを参考にするように。

マスマティカで球面調和関数はSphericalHarmonicY[l, m_l, θ,φ]で表される。
これを使ってSphericalPlot3D[...]で3次元プロットしてみよう。
θとφの範囲はそれぞれ、０からπ、０から2πである。

ただし、波動関数そのものだと虚数部があるのでうまく表示できない。
そこでAbs[ ]により絶対値を取り、その自乗をSphericalPlot3D[ ]でプロットする。
つまり、SphericalPlot3D[Abs[SphericalHarmonicY[l, m_l, θ,φ]]^2, ...]として、波動関数ではなく、存在確率を図示する。

また、曲面が粗い場合は、PlotPoints -> 50と指定して解像度を上げる。
曲面の全部が表示されない場合は、PlotRange -> Allと指定する。

1. l = 0のとき、波動関数（m_l = 0）の存在確率を図示せよ。
2. l = 1のとき、縮退している３つの波動関数（m_l = -1, 0, 1）の存在確率を図示せよ。
   この際、Table[SphericalPlot3D[...], {m_l, -1, 1}]を使用すれば、グラフをいっぺんに出力できる。
3. l = 2のとき、縮退している５つの波動関数（m_l = -2, -1, 0, 1, 2）の存在確率を図示せよ。
   この際、Table[SphericalPlot3D[...], {m_l, -2, 2}]を使用すれば、グラフをいっぺんに出力できる。

課題４　つぎは球面調和関数Y_l,ml (θ,φ)を用いて、水素原子のs 軌道とp 軌道の方位成分を図示してみよう。

1. s軌道はそのまんまY_0,0 (θ, φ)である。
2. p 軌道についてもp_z軌道はまんまY_1,0 (θ,φ)である。
3. ところが、p_x軌道とp_y軌道はつぎのようなY_1,1 (θ,φ) とY_1,-1 (θ,φ) の線形結合で表される。
   　

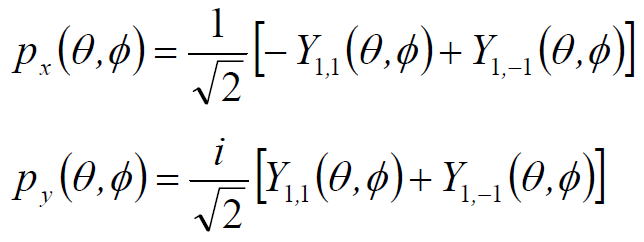
（実際の波動関数はこれらと動径波動関数R_n,l(r) をかけ合わせたものになる）
課題3と同様に、Abs[ ]により絶対値を取り、その自乗をSphericalPlot3D[ ]でプロットする。
つまり、波動関数ではなく、存在確率を図示する。

課題５　つぎは球面調和関数Y_l,ml (θ,φ)を用いて、水素原子のd 軌道の方位成分を表せ。

1. d_z²軌道はそのまんまY_2,0 (θ,φ)である。
2. ところが、残りのd 軌道はつぎのようなY_l,ml (θ,φ)の線形結合で表される。
   　

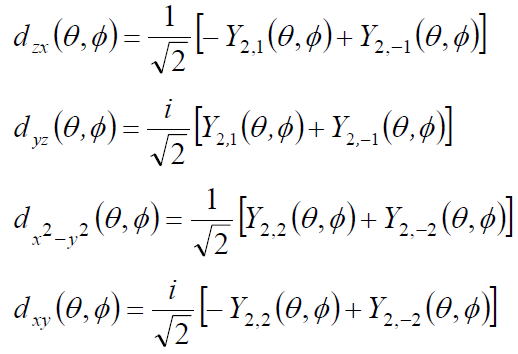
課題3と同様に、Abs[ ]により絶対値を取り、その自乗をSphericalPlot3D[ ]でプロットする。つまり、波動関数ではなく、存在確率を図示する。

課題はマスマティカのファイル（拡張子が.nb）を添付して送ってください。
結果のみではなく、コマンドそのものも送ること。

完成したら、ファイルをメールに添付して提出すること。
送り先：ynagasaあっとfc.ritsumei.ac.jp

• メールのタイトルは”基礎演習２レポート：氏名と学生証番号”とすること。
• 提出ファイルの最初には必ず氏名と学生証番号を記入すること。
• ファイル名は “氏名+171213”とする。（例：立命太郎171213）
  （「.nb」等の拡張子は自動で付くので、自分で書き込む必要はない）
• ファイル名の「氏名」以外は必ず半角。
• 最終締め切り：2017年12月19日（火曜）。
• 日常点評価の提出課題は定期試験と同等の意味があるので真剣に取り組むこと。