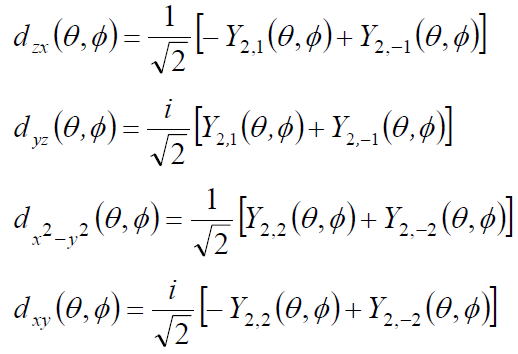Mathematicaを使って量子化学の復習。そして簡単なプログラムについて勉強する。

課題１　球面調和関数Y_l,ml (θ,φ)の図示の復習

1. マスマティカで球面調和関数はSphericalHarmonicY[l, m_l, θ,φ]で表される。
   これを使ってSphericalPlot3D[...]で3次元プロットしてみよう。
   θとφの範囲はそれぞれ、０からπ、０から2πである。
   ただし、波動関数そのものだと虚数部があるのでうまく表示できない。
   そこでAbs[ ]により絶対値を取り、その自乗をSphericalPlot3D[ ]でプロットする。
   つまり、SphericalPlot3D[Abs[SphericalHarmonicY[l, m_l, θ,φ]]^2, ...]として、波動関数ではなく、存在確率を図示する。
   また、曲面が粗い場合は、PlotPoints -> 50と指定して解像度を上げる。
   曲面の全部が表示されない場合は、PlotRange -> Allと指定する。
   　
   l = 2のとき、縮退している５つの波動関数（m_l = -2, -1, 0, 1, 2）の存在確率を図示せよ。
   この際、Table[SphericalPlot3D[...], {m_l, -2, 2}]を使用すれば、グラフをいっぺんに出力できる。
   　
2. つぎは球面調和関数Y_l,ml (θ,φ)を用いて、水素原子のd 軌道の方位成分を表せ。
   d_z²軌道はそのまんまY_2,0 (θ,φ)である。
   残りのd 軌道はつぎのようなY_l,ml (θ,φ)の線形結合で表される。
   　
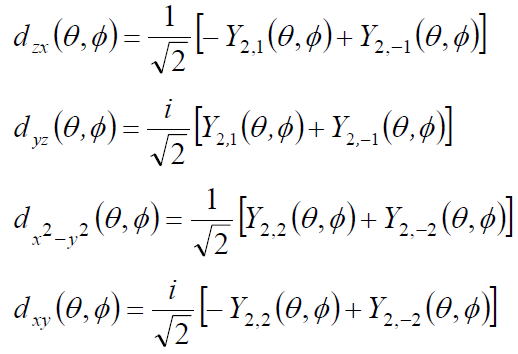
   aと同様に、Abs[ ]により絶対値を取り、その自乗をSphericalPlot3D[ ]でプロットする。つまり、波動関数ではなく、存在確率を図示する。
   

課題2　
０から１０まで数字を表示するプログラムを作る。Print[変数]を使用。

1. While[条件,本体;インクリメント]を使って作る。
   やり方としては、
   まずWhileを行う前に、iの初期値を0とおく（i = 0;）。
   Whileの条件はi <= 10であり、
   本体では、まずiの値をプリントし（Print[i];）、つぎにiの値を１つだけ大きくする（インクリメント： i = i + 1、i++でもできる）。
   この作業をWhileで繰り返す。
   やり方がわからない場合は、ヘルプを見ること。
   　
2. Do[本体, {i, a, b}]を使って作る。aとbはiの初期値（0）と最終値（10）。
   　
3. For[初期値, 条件式, インクリメント, 本体]を使って作る。

課題3
整数aの値を1から５まで変化させて、y=sin[ax], (0<x<2Pi)を次々にグラフ表示せよ。
（以前、Table[　]を使ってやったが、今回は別の方法でやる）
Plotだけではプリントしてくれないので、Print[Plot[関数, {x軸の範囲}]]という形式を使う。

課題4
つぎにコンピューターに大きいか小さいかか判断させる方法を勉強します。（正否の判断）
aとbを比べ、不等式を表示する関数f1[a,b]を作る。

1. If[条件式, 式1, 式2]を使って作る。
   If[条件式, 式1, 式2]は、条件式（a > b）が真(True)ならPrint[a, ">", b]、偽(False)なら、Print[a, "<", b]。
   この方法だと、a=bの場合、「a < b」と表示されて困る。
   　
2. Which[条件式1, 式1, 条件式2, 式2, 条件式3, 式3]を使って作る。
   a == bのときは、Print[a, "<", b]とする。
   　
3. If[ ]の中にIf[ ]を入れて作る。If[条件式1, 式1, If[条件式2, 式1, 式2]]とする。

課題5
関数f(x)を整数０から１０まで１おきに計算し、その値を表示する。
同時に、その値が０より大きい場合「はプラスの数」、同じ場合は「はゼロです。」、小さい場合は「はマイナスの数」と表示するプログラムを作れ。

1. 関数f(x)=(x-5)²-4について、For[ ]にWhich[ ]を組み込み、符号の判定を行う。
   
2. 関数f(x)=(x-4)²-5について、Do[ ]にIf[ ]を組み込み、符号の判定を行う。
   

ランダム関数
マスマティカには任意の実数乱数を発生させるRandom[　]というコマンドがあります。
これを使うと、意外に色々なことができます。

課題6　1次元のランダムウォーク
「酔っぱらいの歩いた経路を表示せよ」という問題。
まず最初の酔っぱらいはx軸に沿って、まっすぐに歩くことができるが、Y軸方向には上下にフラフラする酔っぱらいです。
x軸方向に1進むごとにY軸方向には、＋１、０、−１にふらつきます。
酔っぱらいはどれくらいまっすぐ歩くことができるでしょうか？
　
やり方

1. まずrwalk = { }で中身のないtableを作ります。
2. x = 0; y = 0; i = 0;と変数の初期値を作ります。
3. While[ ]を使い、x の値を１づつ増やし、y の値は-1、0、+1のいずれかの値で変化させます。
4. y の値の変化には、RandomInteger[{-1, 1}]を使います。
5. AppendTo[rwalk, {x, y}]で、(x, y)の座標をrwalkに足していきます。
6. ListPlot[ ]でプロットします。この際、Joined -> Trueとして各座標を線で結びます。

課題7　2次元のランダムウォーク
二番目の酔っぱらいはさらに酔っぱらってて、もうまっすぐ歩くことは不可能です。上下左右に均等な確率で、１づつ歩いていきます。その経路はどうなるでしょう？

やり方

1. 最初は課題6と同じ。
2. RandomInteger[{1, 4}]を使い、1〜4の整数を発生させます。
3. 1，2，3，4のとき、それぞれx-1, x+1, y-1, y+1と値を変化させます。
4. 後は課題6と同じ。

課題8　3次元のランダムウォーク
3次元の酔っぱらいの経路を描きます。
AppendTo[lis, {x, y}]を使う。これは、リストlisの末尾に{x, y}を入れていき、リストの要素を増やしていきます。
　
やり方

1. 最初は課題７と同じですが、今度は3次元なので、x, y, zの座標が必要になります。
2. 課題7と同じ。ただし、今度は1〜6の整数を発生させないといけません。
3. 後は課題7と同じ。

　
　
課題はマスマティカのファイル（拡張子が.nb）を添付して送ってください。
結果のみではなく、コマンドそのものも送ること。

完成したら、ファイルをメールに添付して提出すること。
送り先：ynagasaあっとfc.ritsumei.ac.jp

• メールのタイトルは”基礎演習２レポート：氏名と学生証番号”とすること。
• 提出ファイルの最初には必ず氏名と学生証番号を記入すること。
• ファイル名は “氏名+171220”とする。（例：立命太郎171220）
  （「.nb」等の拡張子は自動で付くので、自分で書き込む必要はない）
• ファイル名の「氏名」以外は必ず半角。
• 最終締め切り：2017年12月25日（月曜）。
• 日常点評価の提出課題は定期試験と同等の意味があるので真剣に取り組むこと。