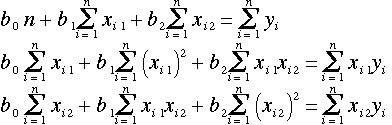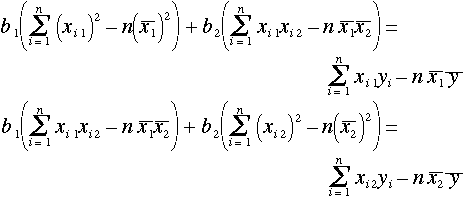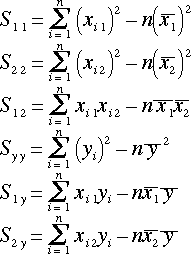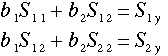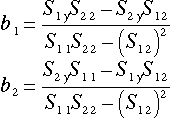重回帰分析による予測モデル
下表に示すような、ひとつの目的変数に対して2つの説明変数がある場合を考える。変数(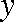 、
、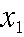 、
、 )の値が
)の値が 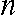 組あり、
組あり、 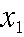 の
の  番目の値は、
番目の値は、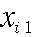 と表記する。
と表記する。

◎ 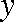 の
の 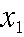 、
、 に対する重回帰式
に対する重回帰式
(1) 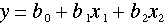
すなわち、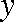 を予測する計算式を求めてみよう。(1)式の中の
を予測する計算式を求めてみよう。(1)式の中の 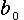 は定数項、
は定数項、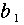 は
は 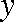 の
の 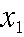 に対する偏回帰係数、
に対する偏回帰係数、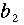 は
は 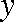 の
の  に対する偏回帰係数という。この重回帰式(1)に実際のデータ(
に対する偏回帰係数という。この重回帰式(1)に実際のデータ( 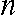 組の
組の 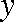 、
、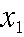 、
、 )を代入して、最も残差(誤差)が少なくなるような係数
)を代入して、最も残差(誤差)が少なくなるような係数 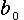 、
、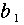 、
、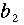 の組み合わせを以下の手順(最小二乗法)で計算することにより、重回帰式(1)を求める。
の組み合わせを以下の手順(最小二乗法)で計算することにより、重回帰式(1)を求める。
◎まず、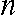 組の中の1番目の
組の中の1番目の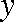 の値と予測計算式の値の差を「実測と予測の残差」として
の値と予測計算式の値の差を「実測と予測の残差」として
(2) 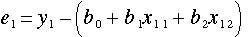
とおく。同様に第  番目の残差は、
番目の残差は、
(3) 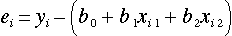
と書くことができる。このような残差の二乗和
(4) 
を最小にする 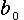 、
、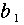 、
、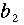 の組み合わせが最小二乗法で求める解となる。
の組み合わせが最小二乗法で求める解となる。
◎(4)式を 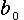 、
、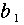 、
、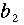 で偏微分してゼロとおく。すなわち、
で偏微分してゼロとおく。すなわち、
(5) 
を得る。これを整理して書き直すと、
(6) 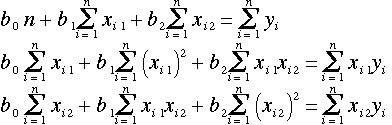
となる。これは、未知数 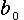 、
、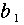 、
、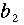 についての3元連立一次方程式であり、通常、正規方程式( normal equation )とよばれる。これを解くには、まず(6)式の第1式を
についての3元連立一次方程式であり、通常、正規方程式( normal equation )とよばれる。これを解くには、まず(6)式の第1式を 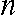 で除し、各変数の平均を用いて
で除し、各変数の平均を用いて 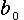 を表す。
を表す。
(7) 
これを(6)式の第2式・第3式に代入して変形すると、
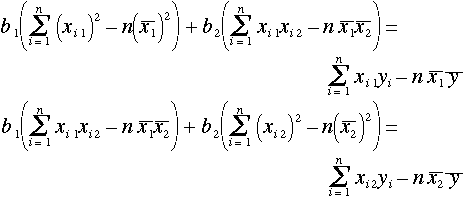
(8)
を得る。これは、未知数 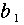 、
、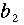 についての2元連立一次方程式であり偏差平方和(変動)と偏差積和(共変動)の公式
についての2元連立一次方程式であり偏差平方和(変動)と偏差積和(共変動)の公式
(9) 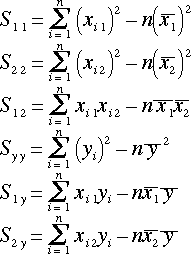
を用いて変形すると、
(10) 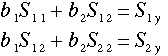
と書くことができる。これより、最小二乗法により求められる重回帰式(1)の偏回帰係数は、
(11) 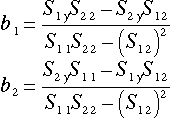
という形で計算することができる。