履歴復元力モデルのプログラミングについて

　非線形地震応答解析をする際，履歴復元力特性をモデル化する必要がある．
どのように履歴復元力特性をプログラミングするか，参考までに一例を示す．
簡単のため，骨格曲線は図1のように2つの傾きで定義される対称型とする．
履歴復元力特性として，鋼構造物でよく用いられる図2のバイリニア型と，コンクリート構造物でよく用いられる図3の剛性劣化型を考える．
剛性劣化型にはいろいろあるが，簡単なClough型モデル（初期剛性で除荷）とする．

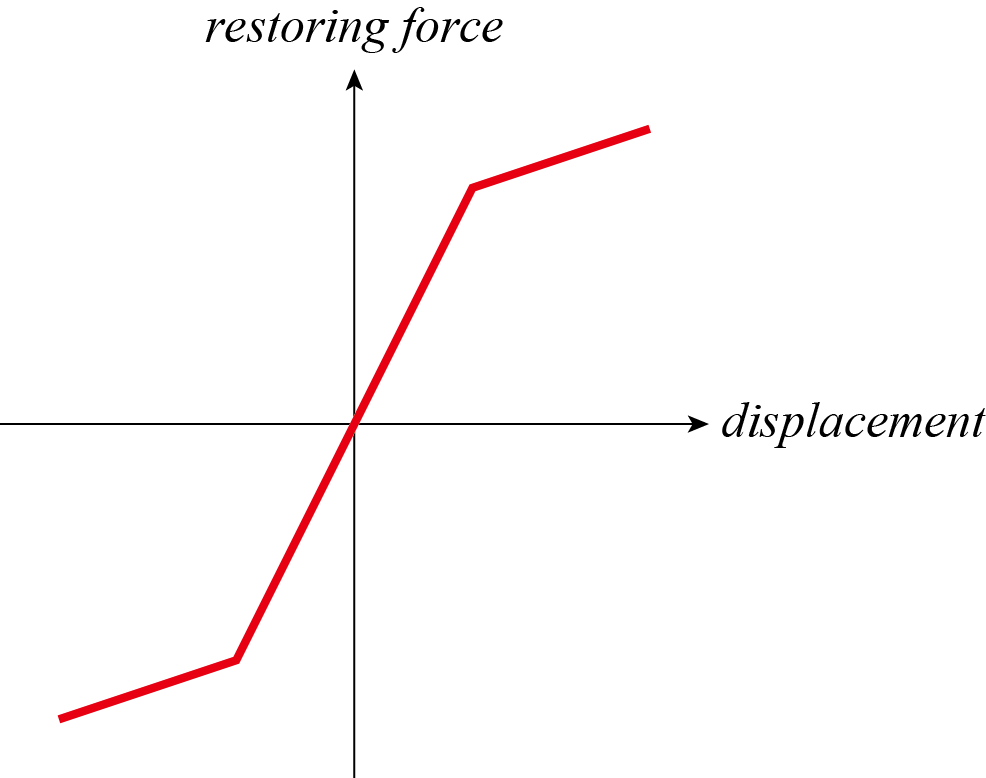　　図1　骨格曲線

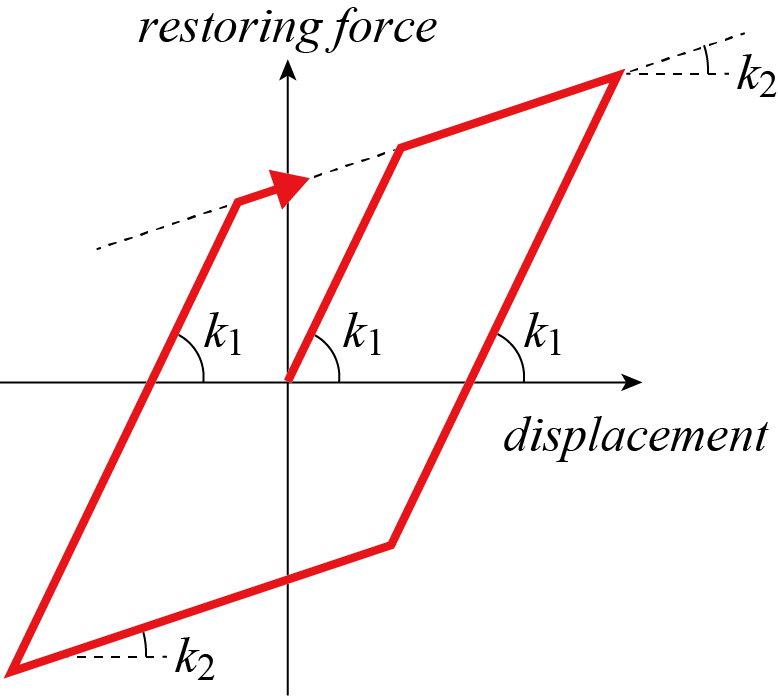　　図2　バイリニア型の履歴曲線

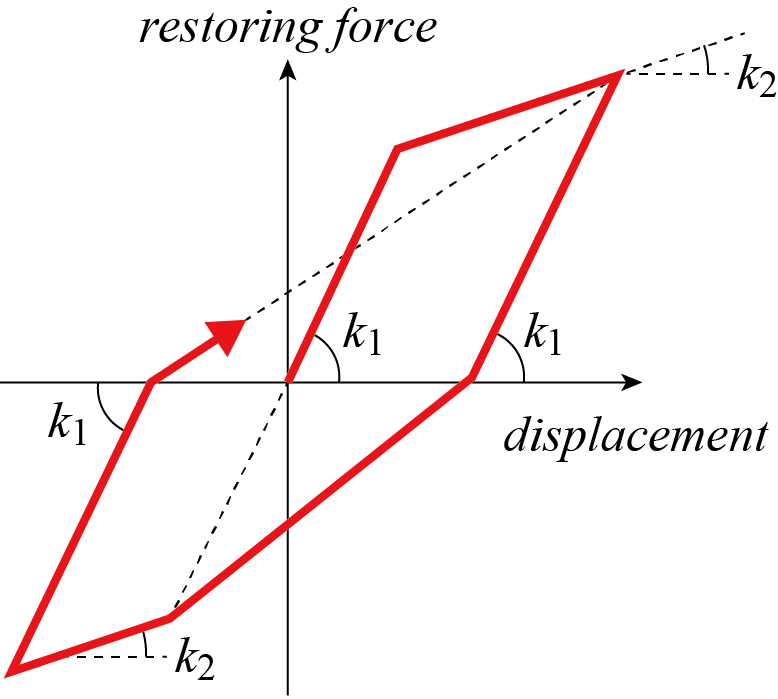　　図3　剛性劣化（Clough）型の履歴曲線

バイリニア・モデル

　次ステップの変位が図4のaまたはbまたはcのように求められたとする．
この場合，復元力として取り得る値は3つである．

・fLは，前ステップの変位から初期剛性k1で変化した場合Lの復元力．
・fUは第二剛性k2で決まる上側の骨格曲線U上の復元力．
・fDは第二剛性k2で決まる下側の骨格曲線D上の復元力．

　fL，fU，fDの大きさを比較し，中央値（最大でも最小でもない値）を次ステップの復元力として採用すればよい．

例：前ステップの変位がxbで復元力がfb，次ステップの変位がxで復元力がf，初期剛性がk1で第二剛性が0，降伏時の復元力がfy（負の側は-fy）の場合．

【Excel VBA】

   fL = k1 * (x - xb) + fb
   If (fL > fy) Then
     f = fy
   ElseIf (fL < -fy) Then
     f = -fy
   Else
     f = fL
   End If

【MATLAB】

function f = bilinear( x, xb, yb, k1, fy )
  fL = k1 * (x - xb) + fb;
  f = median( [ fL fy -fy ] );
end

　第二剛性が0でない場合は，降伏時の変位dyと復元力fyを元に，第二剛性k2を使って骨格曲線上の復元力fUとfDを計算すればよい．

【Excel VBA】

   fL = k1 * (x - xb) + fb
   fU = k2 * (x - dy) + fy
   fD = k2 * (x + dy) - fy
   If (fL > fU) Then
     f = fU
   ElseIf (fL < fD) Then
     f = fD
   Else
     f = fL
   End If

【MATLAB】

function f = bilinear( x, xb, yb, k1, k2, dy, fy )
  fL = k1 * (x - xb) + fb;
  fU = k2 * (x - dy) + fy;
  fD = k2 * (x + dy) - fy;
  f = median( [ fL fU fD ] );
end

　1自由度系非線形地震応答をMATLABで計算するサンプルコードはこちら．

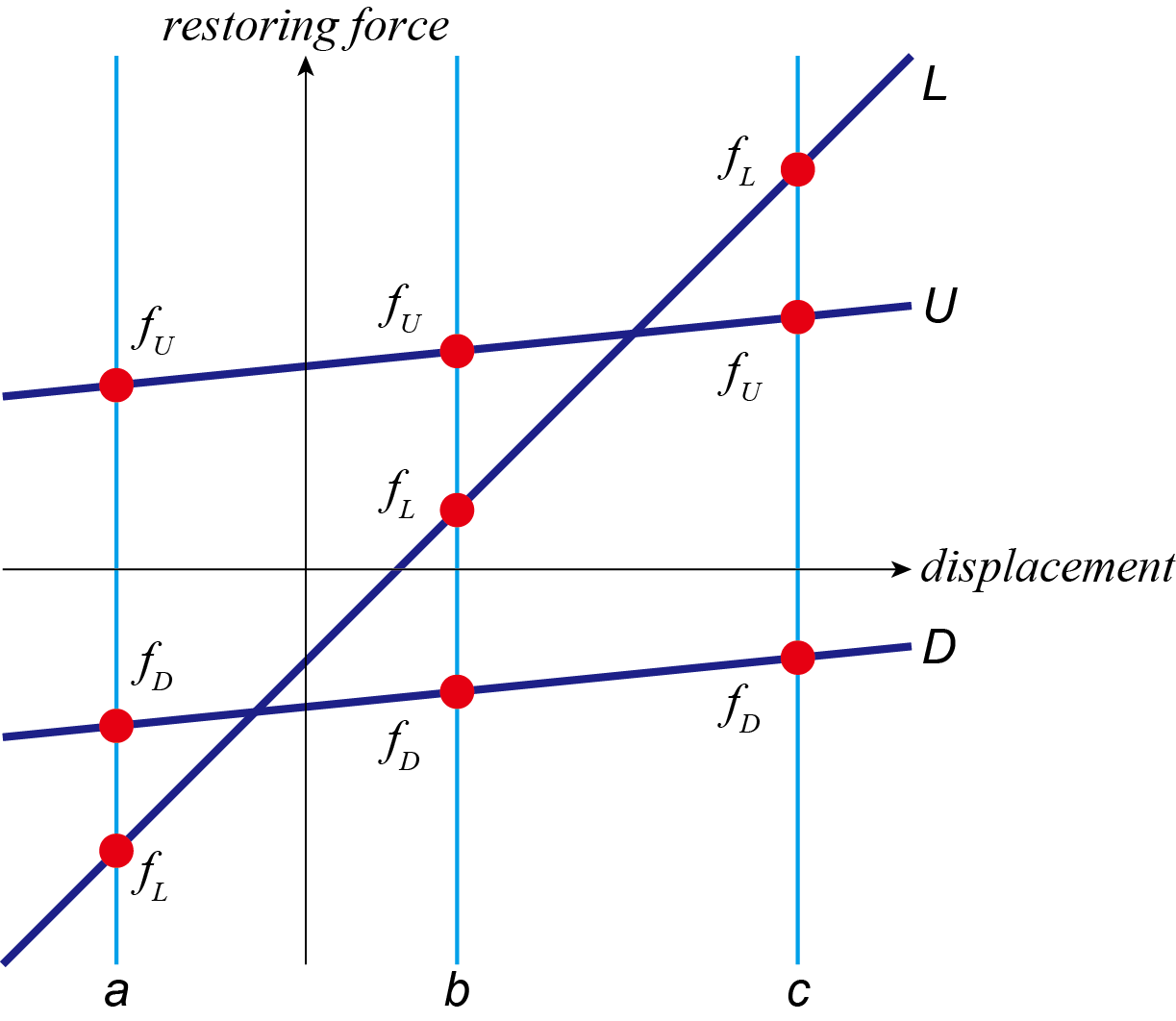　　図4　バイリニア・モデルの考え方

剛性劣化（Clough）モデル

　次ステップの変位が，前ステップの変位よりも大きい時は次のように考える．
まず，前ステップまでの最大点C（初期状態では降伏点とする）を記憶しておく．
図5で，前ステップの位置がA，次ステップの変位がaだとする．

・fLは，前ステップの位置Aから初期剛性で変化した場合Lの復元力．
・f1は，前ステップの位置Aから，直接最大点Cに向かう場合の復元力．
・f2は，前ステップの位置Aから初期剛性で変化する直線Lとx軸との交点Bと，最大点Cを結ぶ線で決まる復元力．

fL，fU，fDの大きさを比較し，中央値をfmとする．
その値fmと，第二剛性で決まる上側の骨格曲線U上の復元力fUとを比較して，小さい方の値を次ステップの復元力fとすればよい．

次ステップの変位が，前ステップの変位よりも小さい時は，上記の最大点を最小点として同じように計算する．
最後に，上側骨格曲線Uではなく下側骨格曲線Dと値を比較し，大きい方の値を次ステップの復元力fとする．

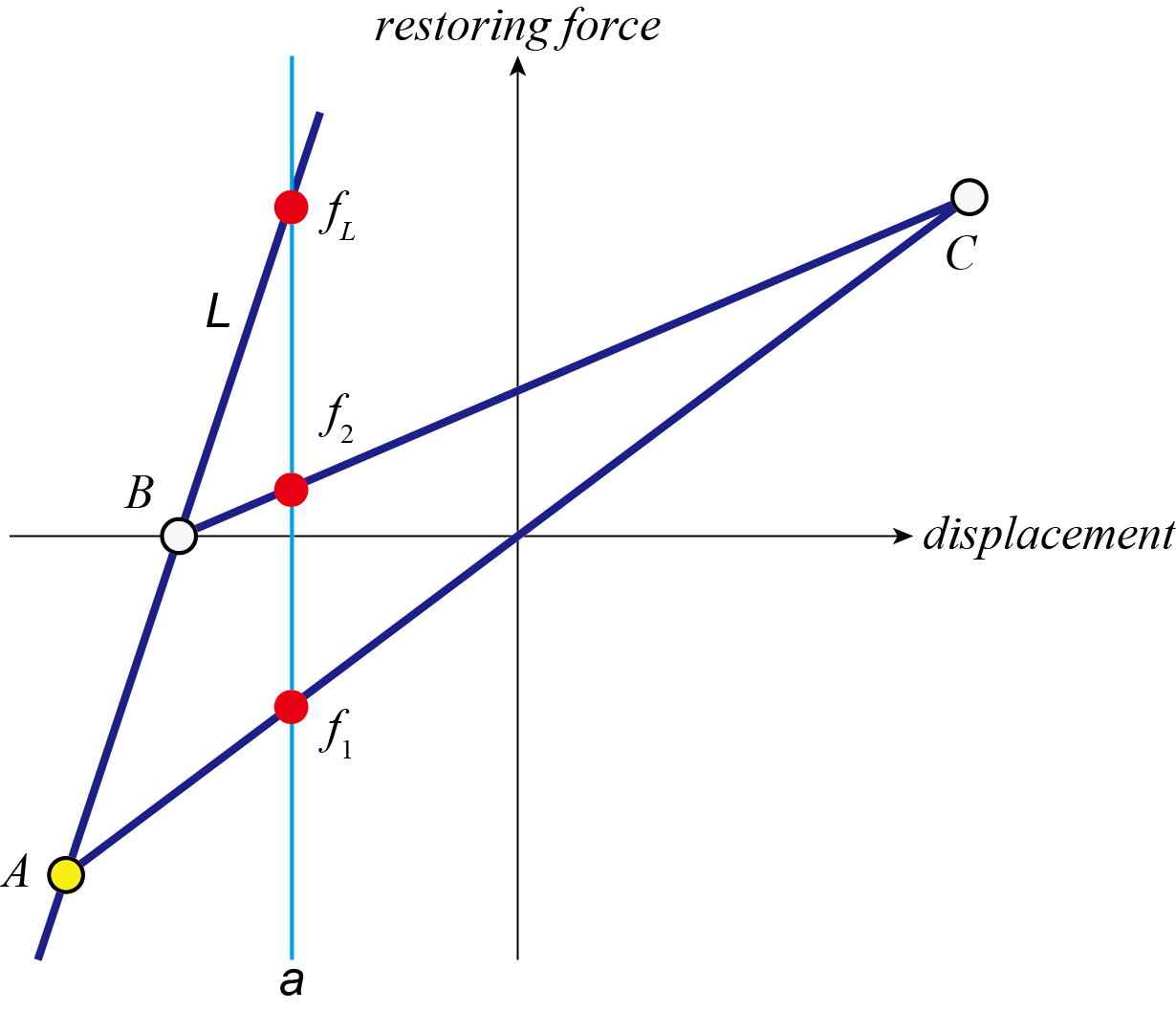　　図5　剛性劣化（Clough）モデルの考え方

　なお，修正武田モデルも，骨格曲線がバイリニアであれば正負の降伏変位を超えた応答に対して上記の「初期剛性」を「初期剛性×（最大あるいは最小応答値の絶対値／降伏変位）の-0.4乗」とすれば計算可能．参考までに，修正武田モデルの復元力を計算するMATLABの関数はこちら．