数学って、どこで役に立つの？「コイン投げ」と「株価予測」の意外な関係
畑翔麻 さん
コハツ-ヒガ・アルトューロ教授
数学って、勉強しても結局のところどこで役立つんだろう…？ そんな疑問を持ったことがある人は、きっと一人や二人じゃないはず。あーあ、勉強でお金が稼げるんだったら、もっと頑張るのになぁ。そんな時、「数学を使って、株価の動きを予測できる」という噂を耳にしました。これを勉強すれば、もしかしてお金持ちになれかもしれない…！ 早速、噂の真相を確かめるため、理工学部理工学研究科の研究室を訪ねました。
― 突然すみません。こちらの研究室では、数学を使って株価の動きを研究していると聞いたのですが……
- え、株価のシミュレーションのことですか？
—はい！なんでも、株の値動きを予測できるという……
- それは確かに研究しています
—その方法を教えていただけませんか？自分も学んで、お金を儲けたいなと
- お、お金儲け？
- ほほー。面白いことを言いますね。ひとまずご説明いたしましょう。まずは大学院生の畑くんに、簡単な例から説明してもらいましょう。畑くん、例のコイン投げの話から、お願いします
- はい、わかりました！ まずは次のようなコイン投げゲームを考えてください
コイン投げと株価の関係
▲コイン投げゲームを例に解説をする理工学研究科の畑さん
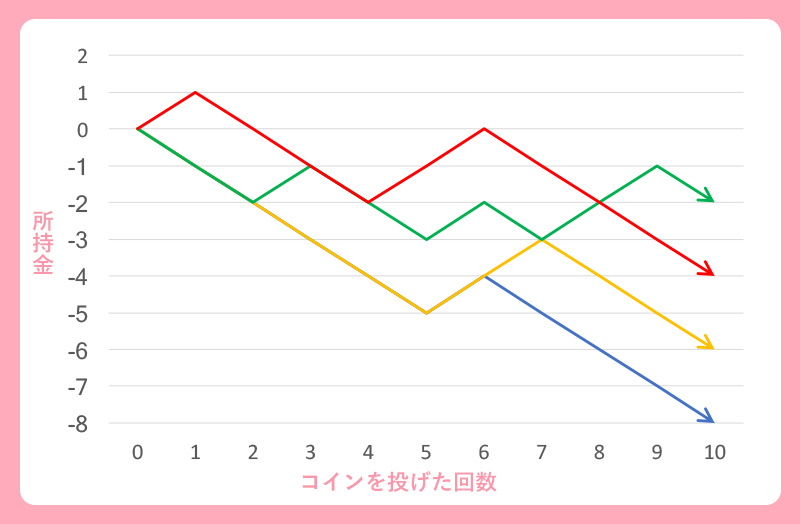
＜0円からスタートして、表が出れば1円もらえて、裏が出たら1円減る。コインを10回投げたときの所持金がいくらになるか。＞
- 表、裏が出る確率はそれぞれ2分の1として、そのゲームを自動的に行うコンピュータプログラムを作ります。１ゲーム終わった時の結果がこのグラフです。
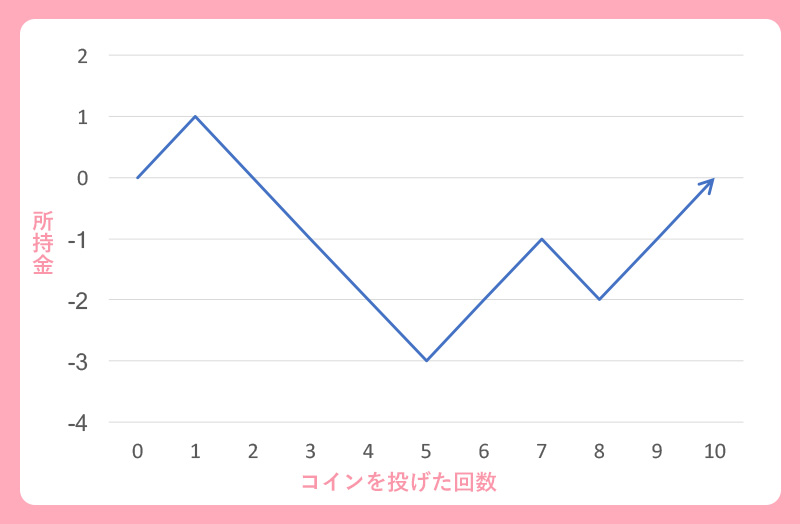▲横軸は投げた回数、縦軸はAくんの所持金。スタートは0円で一回コインを投げるごとに表が出たら1円増えて、裏が出たら1円減っている
- これは、表が5回、裏が5回出た結果、所持金は0円になったことを表しています
—なるほど、了解です。このプログラムでは、コンピュータが自動的にコインを10回投げているのですね。すると、結果は毎回異なるというわけだ
- その通りです。4ゲーム行い、それぞれで得たグラフを重ねて表示したものが次のグラフになります。コインの表、裏が出る確率はそれぞれ1/2なので、グラフは概ね上下均等に動いていますね
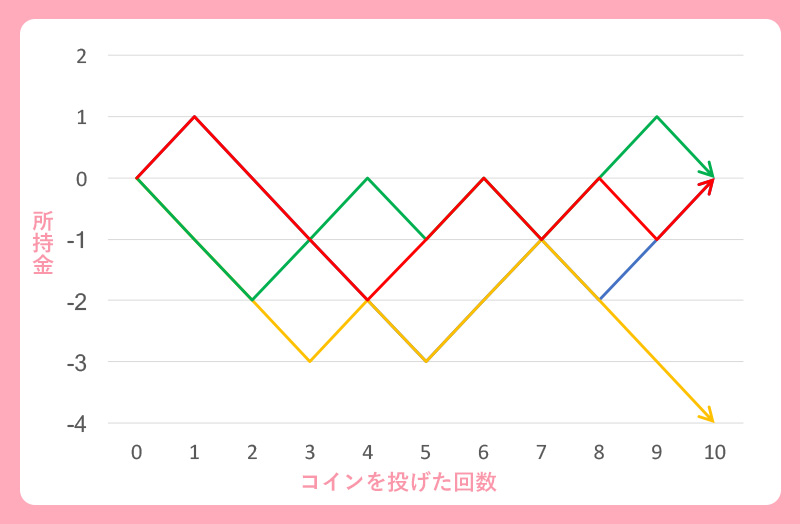▲4回のゲームで得た青、橙、緑、赤の折れ線を重ねて表示
—ふむ、ふむ。これは簡単ですね
- では次に、細工が施されて裏が出やすいコインを使ってゲームをします。表が出る確率は1/4、裏が出る確率は3/4。さっきと同じく、1ゲームだけの結果と、4ゲームの結果を重ねたのが次の2つのグラフです。当然ですが、裏が出やすいため、結果がマイナス側に偏っているのがわかるでしょう
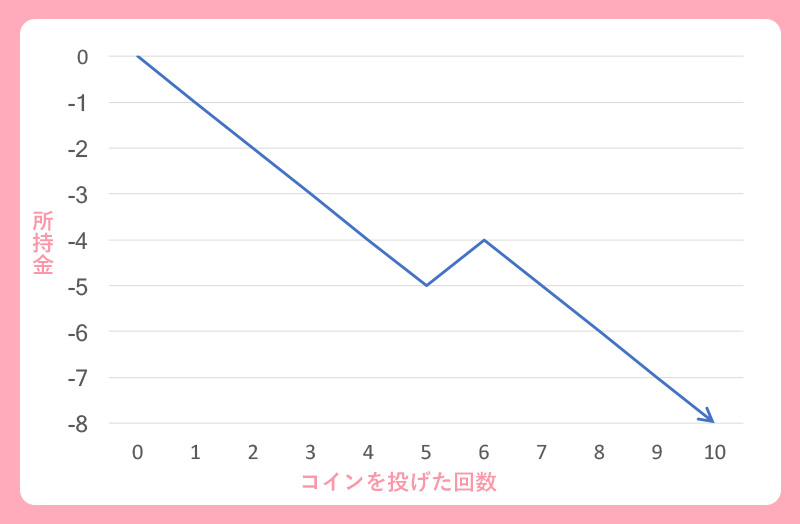
- おわかりいただけましたでしょうか
—よくわかりました。楽勝です。しかし、これと株価では随分話が……
- いや、じつは基本的には同じなんです
—え！ほんとですか？
- そうなんです。株価は毎日上下しますね。日々上がるか下がるかを繰り返して、価格が変わっていくのは、表が出るか裏が出るかを繰り返して所持金が変わるコイン投げと同じでしょう。また、コインの性質によって、表裏ともに出る確率が１/2か、1/4と3/4なのかが決まるように、社会の様々な要因によって、株価が上がりやすいか下がりやすいかが決まるのも同じです
—なるほど、そう考えると、一緒ですね！
- でしょう？ そこでひとまず、株価が具体的にどんな要因で変動するかはおいといて、株価が上下する様子をシミュレーションして見てみましょう。
- スタート時は100円として、365日後にどうなったか。その計算をコイン投げ同様にコンピュータで4回行い、結果を重ねて得たのが次のグラフです
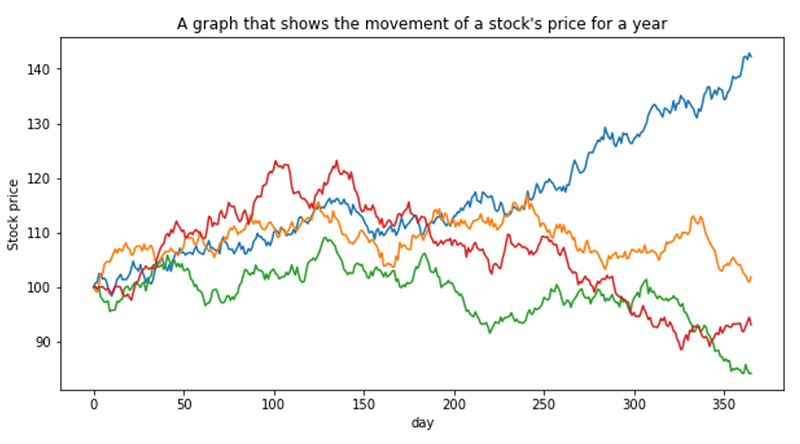▲縦軸は株価、横軸は日数。コイン投げ同様に、各色の折れ線が1回の計算結果を表します
—さっきのコイン投げの結果が複雑になった感じですね
- そうですね。さらに、このグラフから何がわかるかといえば、4回の結果のうち、1年後に100円より大きくなっているのが2回（青とオレンジ）、小さくなっているのが2回（赤と緑）あるのがわかります。つまり、「1年後に損をするリスクは1/2である」ということになるのです。ほら、コイン投げと同じ方法で、株価の動きが予測できました
数学で未来を予測する
—なるほど……。確かにおっしゃる通りなものの、これが何を計算しているのかはよくわからず……
- 先ほどの計算は、『ブラック・ショールズモデル』と呼ばれる理論に従って得た結果です。これは、オプション価格を評価するモデルとして、ブラック先生とショールズ先生によって1973年に発表され、高い評価を受けたものです
—オプション価格、というのは……
- オプション取引においてオプションの権利についてつけられる価格で……
—すみません、言っていることがさっぱりわかりません
- あ、そうですね、いや、気にしないで大丈夫です。とりあえず、ざっくりと株価ということで話を進めましょう。つまり、このような経済に関係する価格などを計算するモデルがいろいろあるんです
—なるほど、モデルがいろいろですか。簡単に言うと、たとえばモデルによってどんな違いがあるのでしょうか
- えーーと……。ちょっと複雑になってきたので、ここからはコハツ先生にバトンタッチをお願いできれば……
- わかりました。では、ここからは私が説明します。難しくならないように、単純化してお話しますね。
- たとえば、先ほどのブラック・ショールズモデルでは、金利を「固定」としています。それを「変動」とすれば、当然計算結果が違ってきます。それも別のモデルです。
また、日本では2016年からマイナス金利政策を導入しました。金利を「変動」とする場合でも、マイナス金利を取り入れた計算をするためには新たなモデルが必要になるわけです。
—ははぁ、なるほど。大変ですね
- このように、現実世界のどんな要素を取り入れるかで、異なるモデルができ、それぞれ別の計算結果を導きます。そして、それらのどの結果が現実とよく合うかを検証することで、モデルの信頼性がわかってきます。畑くんの例では、4回の計算しかしませんでしたが、実際には何十万回と計算を行って、リスクの大きさなどを求めます
—予測のためには、たくさんあるモデルの中から現実に合う1つを選んで計算するのですか？
- いや、そうではありません。1つで完璧なモデルはなく、それぞれに特徴があるので、予測には複数のモデルを用います。つまり、各モデルで計算して得た結果に、モデルの信頼性によって重みをつけて合成するのです。
- たとえば、A、Bという2つのモデルがあって、信頼度が2：1であるとします。モデルAではリスクは30％、モデルBでは10％と計算されたとするとします。その場合、（30×2+10×1）／（2＋1）＝23．3％となります。実際にはもっと複雑ですが、実はみなさんがよく見る天気予報も、これと同じような方法で確率を得ているんですよ
—え、天気予報も同じなんですか？
- そうなんです。天気も、株価と同様に、いろんな要素によって変化します。どうやって台風が成長するか、地形と風、雨はどう関係しているか、それぞれに気象学の理論があります。それを数学で表現してモデル化する。そこに初期条件、たとえば、風速、風向、気温、雲量、雨量などを入力すると、翌日の各値を計算してくれます。ただし、気象のモデルもやはり、どの要素を重視してどの要素は省略するか、そしてどのような計算方法を用いるかでいくつものモデル化の方法があり、各々結果が変わってきます
- 50のモデルがあって、それぞれで翌日の天気を計算したとしますよね。その時、滋賀県は雨になると予測したモデルが10個あったら、単純に言えば、雨が降る確率は10/50＝20％ということになります。実際には先ほどお話ししたように、モデルごとの信頼度が違うため、重みをつけるなどの操作をして、確率が得られます
なぜ「確率」という考え方を入れなければならないか
—なるほど、よくわかりました！一つ不思議なのですが、先ほどのシミュレーションで、ブラック・ショールズモデルでの4回の計算結果がそれぞれ異なっていたように、同じモデルでも計算するたびに異なる結果が出るのはなぜでしょうか
- 重要なところに気が付きましたね。未来のことは、確率的にしか予測ができないことで満ちています。サイコロの出る目は振るたびに異なり、『次は3が出る』と予測できないのと同じです。未来を予測しようとすると、どうしても確率的な考え方が必要になります
—そうか、あくまでも可能性の話をしているわけですもんね
- そう。でも、確率論は予測のためだけではなくて、ほかの分野でも使われる理論なんですよ。例えば、脳の働きや氷河期の説明をするためにも、確率論が不可欠です。……このあたりは、また次の機会にお話ししましょうか
—はい、もう頭がパンクしそうです！ つまり、世の中には、確率的に考えなければならない現象がたくさんある。確定できない要素に対しては、ちゃんと考慮しないといけないということですね
- その通り。たくさんの人が長年研究を積み重ね、様々なモデルをあみ出し、これまでは不可能だった計算を可能にしてきました。それが、現在のように様々な現象の予測に応用できるようになったということですね
—でも、これでお金儲けをするのは、とても先が長いなぁ
- そうですね。予測でお金儲けはちょっと……。でも、数学を活かせる仕事ならたくさんありますよ！ ぼくは、アクチュアリーという、ビジネスにおけるリスクを分析する専門職を目指しているんですが、経済の分野で活躍している先輩はたくさんいます。数学は難しい、と思うかもしれないけど、立命館大学の理工学研究科は、面倒見のいい先生ばかりだし、ちゃんと学べば、しっかり理解できるようになります。実際に式を動かして、深いところを理解できると、数学はとても楽しいですよ
FOLLOW TANQ