(トップにもどる)
data_reg_shingaku2.dtaには以下のような変数が含まれている。
(1)データセットにある各変数間の相関係数を調べよ。
. corr shingaku university income density pop retailing
(obs=47)
| shingaku univer~y income density pop retail~g
-------------+------------------------------------------------------
shingaku | 1.0000
university | 0.4298 1.0000
income | 0.3839 -0.1378 1.0000
density | 0.5215 0.2828 0.1196 1.0000
pop | 0.4150 0.2493 0.0260 0.8391 1.0000
retailing | 0.4290 0.2988 0.0055 0.8622 0.9877 1.0000
pop(人口)とdensity(人口密度)が0.8391、popとretailing(小売業者数)が0.9877と高い相関を持っていることが分かる。
(2)「shingaku(大学・短大への進学率)」を被説明変数として、説明変数として考えられるその他の変数を用いて重回帰分析を行い、多重共線性についても検討せよ。
回帰分析をしたあとでVIFを出力し、さらに結果を保存しておく。
. reg shingaku university income density pop retailing
Source | SS df MS Number of obs = 47
-------------+------------------------------ F( 5, 41) = 8.43
Model | 1176.42691 5 235.285382 Prob > F = 0.0000
Residual | 1144.8828 41 27.9239708 R-squared = 0.5068
-------------+------------------------------ Adj R-squared = 0.4466
Total | 2321.30972 46 50.4632547 Root MSE = 5.2843
------------------------------------------------------------------------------
shingaku | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
university | 12.6327 3.917224 3.22 0.002 4.721703 20.54369
income | .0443032 .0132179 3.35 0.002 .0176091 .0709973
density | .0016358 .0009459 1.73 0.091 -.0002745 .003546
pop | .8856481 2.623102 0.34 0.737 -4.411813 6.183109
retailing | -.1033041 .3027157 -0.34 0.735 -.7146508 .5080427
_cons | 16.25867 7.748805 2.10 0.042 .6096367 31.9077
------------------------------------------------------------------------------
. estat vif
Variable | VIF 1/VIF
-------------+----------------------
retailing | 55.55 0.018001
pop | 46.94 0.021304
density | 4.27 0.233971
university | 1.23 0.813579
income | 1.10 0.907287
-------------+----------------------
Mean VIF | 21.82
. estimates store m0
retailing(小売業者数)とpop(人口)のVIFが高い値を示しており、多重共線性の問題があることが伺われる。両者との相関係数が高かったdensity(人口密度)を含めてこれらを除いたいくつかのモデルを推定し、結果を保存して比較する。
. reg shingaku university income density pop
Source | SS df MS Number of obs = 47
-------------+------------------------------ F( 4, 42) = 10.73
Model | 1173.17498 4 293.293744 Prob > F = 0.0000
Residual | 1148.13474 42 27.3365414 R-squared = 0.5054
-------------+------------------------------ Adj R-squared = 0.4583
Total | 2321.30972 46 50.4632547 Root MSE = 5.2284
------------------------------------------------------------------------------
shingaku | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
university | 12.24066 3.705387 3.30 0.002 4.762891 19.71844
income | .0450952 .012875 3.50 0.001 .0191124 .0710779
density | .0015073 .0008586 1.76 0.086 -.0002254 .0032401
pop | .0239629 .7030473 0.03 0.973 -1.394844 1.44277
_cons | 15.8287 7.564839 2.09 0.042 .5622376 31.09517
------------------------------------------------------------------------------
. estimates store m1
. reg shingaku university income density retailing
Source | SS df MS Number of obs = 47
-------------+------------------------------ F( 4, 42) = 10.73
Model | 1173.24367 4 293.310918 Prob > F = 0.0000
Residual | 1148.06604 42 27.3349058 R-squared = 0.5054
-------------+------------------------------ Adj R-squared = 0.4583
Total | 2321.30972 46 50.4632547 Root MSE = 5.2283
------------------------------------------------------------------------------
shingaku | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
university | 12.25867 3.717479 3.30 0.002 4.756496 19.76085
income | .0448959 .0129619 3.46 0.001 .0187378 .0710541
density | .0015794 .0009211 1.71 0.094 -.0002796 .0034383
retailing | -.0049183 .0811318 -0.06 0.952 -.168649 .1588124
_cons | 16.00415 7.630273 2.10 0.042 .6056341 31.40266
------------------------------------------------------------------------------
. estimates store m2
. reg shingaku university income pop retailing
Source | SS df MS Number of obs = 47
-------------+------------------------------ F( 4, 42) = 9.34
Model | 1092.91598 4 273.228994 Prob > F = 0.0000
Residual | 1228.39374 42 29.24747 R-squared = 0.4708
-------------+------------------------------ Adj R-squared = 0.4204
Total | 2321.30972 46 50.4632547 Root MSE = 5.4081
------------------------------------------------------------------------------
shingaku | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
university | 12.85996 4.006724 3.21 0.003 4.77406 20.94585
income | .0501286 .0130809 3.83 0.000 .0237304 .0765269
pop | .0842441 2.642319 0.03 0.975 -5.248172 5.41666
retailing | .104977 .2842306 0.37 0.714 -.4686235 .6785775
_cons | 12.17547 7.553197 1.61 0.114 -3.067493 27.41844
------------------------------------------------------------------------------
. est store m3
. reg shingaku university income density
Source | SS df MS Number of obs = 47
-------------+------------------------------ F( 3, 43) = 14.65
Model | 1173.14322 3 391.047739 Prob > F = 0.0000
Residual | 1148.1665 43 26.7015465 R-squared = 0.5054
-------------+------------------------------ Adj R-squared = 0.4709
Total | 2321.30972 46 50.4632547 Root MSE = 5.1674
------------------------------------------------------------------------------
shingaku | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
university | 12.24042 3.662091 3.34 0.002 4.855111 19.62573
income | .0450356 .0126069 3.57 0.001 .0196114 .0704598
density | .0015316 .0004731 3.24 0.002 .0005776 .0024857
_cons | 15.88585 7.290539 2.18 0.035 1.183073 30.58862
------------------------------------------------------------------------------
. est store m4
. estimates table *, b(%9.3fc) star stat(N r2)
--------------------------------------------------------------------------
Variable | m0 m1 m2 m3
-------------+------------------------------------------------------------
university | 12.633** 12.241** 12.259** 12.860**
income | 0.044** 0.045** 0.045** 0.050***
density | 0.002 0.002 0.002
pop | 0.886 0.024 0.084
retailing | -0.103 -0.005 0.105
_cons | 16.259* 15.829* 16.004* 12.175
-------------+------------------------------------------------------------
N | 47 47 47 47
r2 | 0.507 0.505 0.505 0.471
--------------------------------------------------------------------------
legend: * p<0.05; ** p<0.01; *** p<0.001
-----------------------------
Variable | m4
-------------+---------------
university | 12.240**
income | 0.045***
density | 0.002**
pop |
retailing |
_cons | 15.886*
-------------+---------------
N | 47
r2 | 0.505
-----------------------------
legend: * p<0.05; ** p<0.01; *** p<0.001
popとretailingの両者を除いたモデル(m4)でのみ、density変数が1%水準で有意になる。ここでは表示していないが、3つのうち2つを除外すると、残りの一つが有意になる。こういう場合は各変数の効果をデータから判断することが難しいので、理論的に意味のある解釈が成立する変数を残す、といった判断も考えられるだろう。
問題:本章のデータts.dtaを用い,完全失業率uerの対数系列について,1変量時系列モデルによる分析をする.
(1) 単位根の検定を行え.
データを読み込み,完全失業率の対数系列luerを作成する.
. use data_ts.dta . gen luer=ln(uer)
コレログラムを確認すると以下のようになる.
. corrgram luer
-1 0 1 -1 0 1
-1 0 1 -1 0 1
LAG AC PAC Q Prob>Q [Autocorrelation] [Partial Autocor]
-------------------------------------------------------------------------------
1 0.9444 0.9971 53.556 0.0000 |------- |-------
2 0.8896 -0.3513 101.94 0.0000 |------- --|
3 0.8426 0.2502 146.16 0.0000 |------ |--
4 0.7835 -0.3074 185.1 0.0000 |------ --|
5 0.7070 0.0483 217.43 0.0000 |----- |
6 0.6331 0.1343 243.86 0.0000 |----- |-
7 0.5601 0.1463 264.96 0.0000 |---- |-
8 0.4809 -0.0270 280.83 0.0000 |--- |
9 0.4037 0.0465 292.24 0.0000 |--- |
10 0.3292 -0.1146 300 0.0000 |-- |
11 0.2588 0.2599 304.89 0.0000 |-- |--
12 0.1951 -0.1548 307.74 0.0000 |- -|
13 0.1434 0.1409 309.31 0.0000 |- |-
14 0.0972 0.1026 310.05 0.0000 | |
15 0.0673 0.3164 310.41 0.0000 | |--
16 0.0490 -0.0011 310.61 0.0000 | |
17 0.0295 -0.2925 310.68 0.0000 | --|
18 0.0100 -0.0963 310.69 0.0000 | |
19 -0.0042 0.1662 310.69 0.0000 | |-
20 -0.0156 0.2984 310.71 0.0000 | |--
21 -0.0407 0.2328 310.87 0.0000 | |-
22 -0.0725 0.2050 311.37 0.0000 | |-
23 -0.1045 0.3477 312.45 0.0000 | |--
24 -0.1417 -0.1969 314.5 0.0000 -| -|
25 -0.1787 0.3178 317.86 0.0000 -| |--
26 -0.2136 0.4011 322.8 0.0000 -| |---
単位根検定の結果は以下である.
. dfgls luer
DF-GLS for luer Number of obs = 46
Maxlag = 10 chosen by Schwert criterion
DF-GLS tau 1% Critical 5% Critical 10% Critical
[lags] Test Statistic Value Value Value
------------------------------------------------------------------------------
10 -1.166 -3.743 -2.701 -2.414
9 -1.657 -3.743 -2.754 -2.470
8 -1.429 -3.743 -2.812 -2.528
7 -1.401 -3.743 -2.871 -2.587
6 -1.212 -3.743 -2.931 -2.645
5 -1.253 -3.743 -2.991 -2.702
4 -1.554 -3.743 -3.048 -2.756
3 -1.859 -3.743 -3.101 -2.805
2 -1.380 -3.743 -3.148 -2.849
1 -1.591 -3.743 -3.189 -2.886
Opt Lag (Ng-Perron seq t) = 3 with RMSE .0850891
Min SC = -4.645961 at lag 1 with RMSE .0901562
Min MAIC = -4.649544 at lag 1 with RMSE .0901562
以上からレベルの対数完全失業率には単位根があることがわかる.
(2) モデル選択を行い,最適なモデルで推定を行え.
単位根を解消するために1次の差分系列で推定を行うが,ここでモデル選択を行う.
最初に自己相関を見ると1次のラグで95%信頼区間から出ているが,それ以上のラグについては信頼区間内に入っている.
. ac d.luer
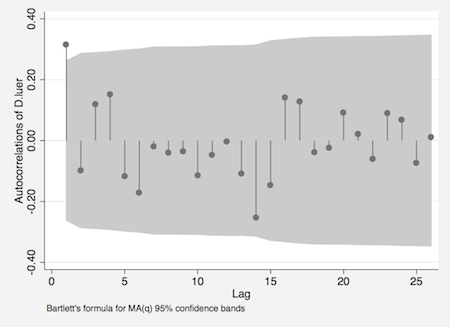
偏自己相関については,1次と3次のほか,高次のラグでいくつか95%信頼区間から出ている.ここでは3次のラグまで考慮する.
. pac d.luer
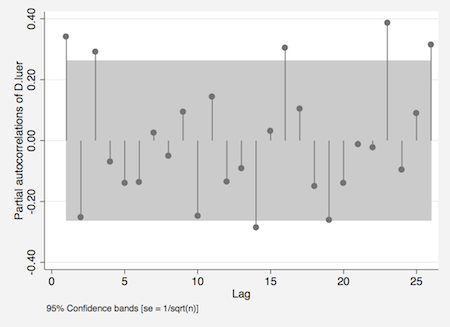
以上の結果から,3つのモデルについて比較する.
. quietly arima luer, arima(3, 1, 1)
. estimates store arima1
. quietly arima luer, arima(2, 1, 1)
. estimates store arima2
. quietly arima luer, arima(1, 1, 1)
. estimates store arima3
. estimates stats arima1 arima2 arima3
-----------------------------------------------------------------------------
Model | Obs ll(null) ll(model) df AIC BIC
-------------+---------------------------------------------------------------
arima1 | 56 . 52.17249 6 -92.34499 -80.19288
arima2 | 56 . 52.16101 5 -94.32201 -84.19525
arima3 | 56 . 52.08476 4 -96.16953 -88.06812
-----------------------------------------------------------------------------
Note: N=Obs used in calculating BIC; see [R] BIC note
AIC,BICの結果からarima(1, 1, 1)が選択される.推定結果は以下のとおり.
. estimates replay arima3
----------------------------------------------------------------------------------
Model arima3
----------------------------------------------------------------------------------
ARIMA regression
Sample: 1954 - 2009 Number of obs = 56
Wald chi2(2) = 120.36
Log likelihood = 52.08476 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
| OPG
D.luer | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
luer |
_cons | .0199033 .0183233 1.09 0.277 -.0160097 .0558163
-------------+----------------------------------------------------------------
ARMA |
ar |
L1. | -.3330407 .1462926 -2.28 0.023 -.619769 -.0463125
|
ma |
L1. | 1.128159 .1316987 8.57 0.000 .8700342 1.386284
-------------+----------------------------------------------------------------
/sigma | .0838974 .0129742 6.47 0.000 .0584684 .1093264
------------------------------------------------------------------------------
(3) (2)の推定結果を使って2040年までの予測を行え.
サンプルを2040年分まで作成する.
. set obs 88 obs was 57, now 88 . replace year=[_n+1952] (31 real changes made)
予測を行い,実現値と予測値をグラフに表示する.
. tsline luer pluer

問題:本章で使用したデータ(data_cat.dta)を用いて,booksを被説明変数,educを説明変数として順序ロジスティック回帰を行う.
(1) 推定した結果の解釈を行え.
はじめにtabulateコマンドでbooksの分布を確認しておくとよいだろう.
. tabulate books
books | Freq. Percent Cum.
------------+-----------------------------------
1 | 664 50.73 50.73
2 | 420 32.09 82.81
3 | 225 17.19 100.00
------------+-----------------------------------
Total | 1,309 100.00
次に順序ロジスティック回帰を実行する.
. ologit books i.educ
Iteration 0: log likelihood = -1324.3286
Iteration 1: log likelihood = -1261.6634
Iteration 2: log likelihood = -1261.1503
Iteration 3: log likelihood = -1261.15
Iteration 4: log likelihood = -1261.15
Ordered logistic regression Number of obs = 1309
LR chi2(2) = 126.36
Prob > chi2 = 0.0000
Log likelihood = -1261.15 Pseudo R2 = 0.0477
------------------------------------------------------------------------------
books | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
educ |
2 | .7341558 .1456046 5.04 0.000 .4487761 1.019536
3 | 1.4786 .1366 10.82 0.000 1.210869 1.746331
-------------+----------------------------------------------------------------
/cut1 | .4351751 .0702629 .2974623 .5728879
/cut2 | 2.109665 .0940615 1.925308 2.294022
------------------------------------------------------------------------------
(Version 10以前のStataだとコマンドの最初にxiプリフィクスをつける.)
短大卒の人は「1ヶ月の間に本を読まない」と「本を1から3冊読む」のうち,「本を1から3冊読む」と回答するオッヅが高卒の人に比べて約2(=exp(734))倍であることがわかる.
モデルを比較のために保存しておく.
. quietly fitstat, saving(mod1)
(2) (1)のモデルの結果を保存せよ.次に,lninc2を付加したモデルを実行し,結果を保存せよ.二つのモデルの適合度を比較せよ.
lninc2を入れたモデルを作成し.結果をはじめのモデルと比較する.
. ologit books i.educ lninc2
Iteration 0: log likelihood = -1324.3286
Iteration 1: log likelihood = -1254.3796
Iteration 2: log likelihood = -1253.8127
Iteration 3: log likelihood = -1253.8123
Iteration 4: log likelihood = -1253.8123
Ordered logistic regression Number of obs = 1309
LR chi2(3) = 141.03
Prob > chi2 = 0.0000
Log likelihood = -1253.8123 Pseudo R2 = 0.0532
------------------------------------------------------------------------------
books | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
educ |
2 | .6235433 .1487022 4.19 0.000 .3320924 .9149941
3 | 1.341758 .141133 9.51 0.000 1.065142 1.618373
|
lninc2 | .4311248 .1135051 3.80 0.000 .2086588 .6535907
-------------+----------------------------------------------------------------
/cut1 | 6.049088 1.481274 3.145844 8.952331
/cut2 | 7.735795 1.486973 4.821382 10.65021
------------------------------------------------------------------------------
. fitstat, using(mod1)
Measures of Fit for ologit of books
Current Saved Difference
Model: ologit ologit
N: 1309 1309 0
Log-Lik Intercept Only -1324.329 -1324.329 0.000
Log-Lik Full Model -1253.812 -1261.150 7.338
D 2507.625(1303) 2522.300(1304) 14.675(1)
LR 141.033(3) 126.357(2) 14.675(1)
Prob > LR 0.000 0.000 0.000
McFadden's R2 0.053 0.048 0.006
McFadden's Adj R2 0.049 0.044 0.005
ML (Cox-Snell) R2 0.102 0.092 0.010
Cragg-Uhler(Nagelkerke) R2 0.118 0.106 0.012
McKelvey & Zavoina's R2 0.108 0.097 0.011
Variance of y* 3.687 3.642 0.045
Variance of error 3.290 3.290 0.000
Count R2 0.542 0.540 0.002
Adj Count R2 0.070 0.067 0.003
AIC 1.925 1.935 -0.010
AIC*n 2519.625 2532.300 -12.675
BIC -6844.031 -6836.532 -7.498
BIC' -119.502 -112.003 -7.498
BIC used by Stata 2543.510 2551.008 -7.498
AIC used by Stata 2517.625 2530.300 -12.675
Difference of 7.498 in BIC' provides strong support for current model.
Note: p-value for difference in LR is only valid if models are nested.
fitstatの結果に示されるとおり,lninc2を含むモデルの方が適切である.学歴を考慮しても,収入の高い人の方が,読書量が多いグループに入る傾向があることがこのモデルから示唆される.
問題:data_ldv_practice.dtaは病院への通院回数(月あたり)のデータである.通院回数について,以下のモデルを用いて推定を行う.
![]()
(1) ポワソン回帰(poisson)で推定し,モデルのフィットを確認せよ.
推定に先だって通院回数(dcvis)の分布を確認しておくと,0回が最も比率が高く,2回までで全体の70%近くを占めていることがわかる.
. tabulate dcvis
number of |
doctor |
visits | Freq. Percent Cum.
------------+-----------------------------------
0 | 353 35.30 35.30
1 | 219 21.90 57.20
2 | 114 11.40 68.60
3 | 74 7.40 76.00
4 | 68 6.80 82.80
5 | 46 4.60 87.40
6 | 32 3.20 90.60
7 | 31 3.10 93.70
8 | 25 2.50 96.20
9 | 18 1.80 98.00
10 | 12 1.20 99.20
11 | 8 0.80 100.00
------------+-----------------------------------
Total | 1,000 100.00
ポワソン回帰の推定結果は以下のとおり.
. poisson dcvis age female married inc, nolog
Poisson regression Number of obs = 1000
LR chi2(4) = 264.97
Prob > chi2 = 0.0000
Log likelihood = -2311.3335 Pseudo R2 = 0.0542
------------------------------------------------------------------------------
dcvis | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age | .0166808 .0021309 7.83 0.000 .0125044 .0208572
female | .539967 .0452597 11.93 0.000 .4512597 .6286743
married | .1633433 .0473191 3.45 0.001 .0705995 .256087
inc | .0003811 .0000628 6.07 0.000 .0002581 .0005042
_cons | -.4763869 .1005565 -4.74 0.000 -.673474 -.2792999
------------------------------------------------------------------------------
. estat gof
Goodness-of-fit chi2 = 2792.746
Prob > chi2(995) = 0.0000
モデルのフィットを確認したところ上に示されるように,ポワソン回帰モデルは適切ではないことが示された.この推定結果をpregで保存する.
. estimates store preg
(2) 負の2項回帰(nb1,nb2)で推定せよ.
次に負の二項回帰モデルによる推定を行う.最初に,NB2の結果を示す.
. nbreg dcvis age female married inc, nolog
Negative binomial regression Number of obs = 1000
LR chi2(4) = 86.36
Dispersion = mean Prob > chi2 = 0.0000
Log likelihood = -1921.3426 Pseudo R2 = 0.0220
------------------------------------------------------------------------------
dcvis | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age | .0189164 .0038799 4.88 0.000 .0113119 .026521
female | .5878782 .0810392 7.25 0.000 .4290444 .7467121
married | .1803937 .0850096 2.12 0.034 .0137778 .3470095
inc | .0004693 .000134 3.50 0.000 .0002067 .000732
_cons | -.6402029 .1805987 -3.54 0.000 -.9941699 -.2862359
-------------+----------------------------------------------------------------
/lnalpha | .0488437 .0769593 -.1019937 .1996811
-------------+----------------------------------------------------------------
alpha | 1.050056 .0808115 .9030353 1.221013
------------------------------------------------------------------------------
Likelihood-ratio test of alpha=0: chibar2(01) = 779.98 Prob>=chibar2 = 0.000
推定結果をnb2に残す.
. estimates store nb2
続いてNB1の推定結果である.
. nbreg dcvis age female married inc, dispersion(constant) nolog
Negative binomial regression Number of obs = 1000
LR chi2(4) = 124.74
Dispersion = constant Prob > chi2 = 0.0000
Log likelihood = -1902.1541 Pseudo R2 = 0.0317
------------------------------------------------------------------------------
dcvis | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age | .0178084 .0034775 5.12 0.000 .0109927 .0246242
female | .5846776 .0731212 8.00 0.000 .4413627 .7279925
married | .1247276 .0753394 1.66 0.098 -.0229348 .2723901
inc | .0004848 .0000956 5.07 0.000 .0002975 .0006722
_cons | -.5665201 .1604945 -3.53 0.000 -.8810836 -.2519566
-------------+----------------------------------------------------------------
/lndelta | .8243906 .0853159 .6571745 .9916067
-------------+----------------------------------------------------------------
delta | 2.280491 .1945621 1.929333 2.695562
------------------------------------------------------------------------------
Likelihood-ratio test of delta=0: chibar2(01) = 818.36 Prob>=chibar2 = 0.000
推定結果をnb1として残す.
. estimates store nb1
(3) 上で推定した3つのモデルを比較せよ.
3つのモデルの推定係数およびモデル統計量を以下に示した.
. estimates table preg nb2 nb1, star stats(ll aic bic)
--------------------------------------------------------------
Variable | preg nb2 nb1
-------------+------------------------------------------------
dcvis |
age | .01668078*** .01891641*** .01780844***
female | .53996702*** .58787823*** .5846776***
married | .16334326*** .18039367* .12472763
inc | .00038113*** .00046935*** .00048484***
_cons | -.47638693*** -.64020291*** -.56652012***
-------------+------------------------------------------------
lnalpha |
_cons | .04884372
-------------+------------------------------------------------
lndelta |
_cons | .82439061***
-------------+------------------------------------------------
Statistics |
ll | -2311.3335 -1921.3426 -1902.1541
aic | 4632.6671 3854.6853 3816.3081
bic | 4657.2058 3884.1318 3845.7547
--------------------------------------------------------------
legend: * p<0.05; ** p<0.01; *** p<0.001
対数尤度,AIC,BICのいずれもNB1が最も適切であることを示している.係数の有意性については,いずれのモデルも同じ結果を示している.NB1の結果から,平均値での年齢の限界効果を確認する.
. quietly nbreg dcvis age female married inc, dispersion(constant) nolog
. margins, dydx(age) atmeans
Conditional marginal effects Number of obs = 1000
Model VCE : OIM
Expression : Predicted number of events, predict()
dy/dx w.r.t. : age
at : age = 40.872 (mean)
female = .475 (mean)
married = .655 (mean)
inc = 351.2612 (mean)
------------------------------------------------------------------------------
| Delta-method
| dy/dx Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age | .035543 .006887 5.16 0.000 .0220448 .0490412
------------------------------------------------------------------------------
年齢が10歳上昇した場合,通院回数が0.355(0.0355×10)回,増加することがわかる.
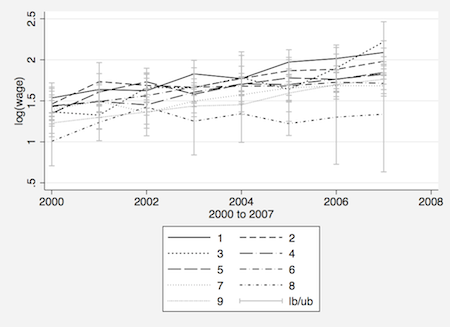
(1) 本章で使用したdata_xt_2.dtaを使い,2000〜2007年すべての調査期間に回答したサンプルに限定し,業種別(occ1〜occ9)に賃金(対数値:lwage)の推移を図示せよ.
全年度(2000〜2007年)回答しているかどうかを判断するために,idごとに何年に回答があるかを示す変数(sum_d)をあらかじめ作る.また,occ1〜occ9のダミーを一つにまとめた変数(occ)もつくっておく.
. gen d=1
. sort id year
. by id : egen sum_d=sum(d)
. gen occ=.
(3515 missing values generated)
. forvalues i =1(1)9 {
replace occ=`i' if occ`i'==1
}
(363 real changes made)
(322 real changes made)
(189 real changes made)
(378 real changes made)
(721 real changes made)
(706 real changes made)
(329 real changes made)
(59 real changes made)
(448 real changes made)
. xtset id year
panel variable: id (unbalanced)
time variable: year, 2000 to 2007
delta: 1 unit
. xtgraph lwage if sum_d==8, av(mean) group(occ)
(2) 以下の説明変数群を用いて,賃金関数を3つの線形回帰モデル(プーリング推計, 固定効果推計,変量効果推定)で推計しなさい(レファレンス変数として, occ9[職種], d07[調査年]を用いる).説明変数群:educ exper expersq union d01-d06 occ1-occ8
. quietly reg lwage educ exper expersq union d01-d06 occ1-occ8
. estimates store PL
. quietly xtreg lwage educ exper expersq union d01-d06 occ1-occ8, fe
. estimates store FE
. quietly xtreg lwage educ exper expersq union d01-d06 occ1-occ8, re
. estimates store RE
. estimates table PL FE RE, stat(N) star
--------------------------------------------------------------
Variable | PL FE RE
-------------+------------------------------------------------
educ | .08857238*** (omitted) .09494866***
exper | .09429149*** .13975001*** .12954507***
expersq | -.00311575*** -.0055037*** -.00501305***
union | .19572994*** .09909261*** .12220483***
d01 | .00801284 .016029 .01226658
d02 | -.0080259 -.01586619 -.01585324
d03 | -.02331957 -.04769533* -.04440843
d04 | -.02597335 -.05744433* -.05193071*
d05 | -.01137255 -.05106687* -.04324729
d06 | .00376287 -.03506508 -.02713294
occ1 | .29146005*** .06171286 .12748243***
occ2 | .25675664*** .02363906 .09079543*
occ3 | .2148385*** -.03772692 .03335481
occ4 | .14089617*** -.04700733 .00711674
occ5 | .20834739*** -.01733444 .0495672
occ6 | .15403759*** -.02412722 .0308353
occ7 | .08142965* -.03152133 .0062851
occ8 | -.11783606 -.0582498 -.0704941
_cons | -.0612237 1.0170361*** -.11233344
-------------+------------------------------------------------
N | 3515 3515 3515
--------------------------------------------------------------
legend: * p<0.05; ** p<0.01; *** p<0.001
(3) 検定の結果,どのモデルが採択されるか答えよ.
まずプーリング・モデルと固定効果モデルの結果を比較する.
. xtreg lwage educ exper expersq union d01-d06 occ1-occ8, fe note: educ omitted because of collinearity (中略) F test that all u_i=0: F(544, 2953) = 6.09 Prob > F = 0.0000
「個別効果がない(u_i=0)」という帰無仮説が棄却されたため,固定効果が採用された.
次にプーリング・モデルと変量効果モデルの結果を比較する.
. quietly xtreg lwage educ exper expersq union d01-d06 occ1-occ8, re
. xttest0
Breusch and Pagan Lagrangian multiplier test for random effects
lwage[id,t] = Xb + u[id] + e[id,t]
Estimated results:
| Var sd = sqrt(Var)
---------+-----------------------------
lwage | .290275 .5387718
e | .1317872 .3630251
u | .1102739 .3320751
Test: Var(u) = 0
chi2(1) = 1920.11
Prob > chi2 = 0.0000
「個体間分散がない(Var(u))=0」という帰無仮説が棄却されたため,変量効果モデルが採用された.
最後に固定効果モデルと変量効果モデルを比較する.
. quietly xtreg lwage educ exper expersq union d01-d06 occ1-occ8, re
. hausman FE
---- Coefficients ----
| (b) (B) (b-B) sqrt(diag(V_b-V_B))
| FE . Difference S.E.
-------------+----------------------------------------------------------------
exper | .13975 .1295451 .0102049 .0034182
expersq | -.0055037 -.005013 -.0004907 .0002558
union | .0990926 .1222048 -.0231122 .0102408
d01 | .016029 .0122666 .0037624 .0043259
d02 | -.0158662 -.0158532 -.0000129 .0041064
d03 | -.0476953 -.0444084 -.0032869 .0037718
d04 | -.0574443 -.0519307 -.0055136 .0032142
d05 | -.0510669 -.0432473 -.0078196 .0026906
d06 | -.0350651 -.0271329 -.0079321 .0026061
occ1 | .0617129 .1274824 -.0657696 .015219
occ2 | .0236391 .0907954 -.0671564 .0137496
occ3 | -.0377269 .0333548 -.0710817 .0167891
occ4 | -.0470073 .0071167 -.0541241 .0141177
occ5 | -.0173344 .0495672 -.0669016 .0152267
occ6 | -.0241272 .0308353 -.0549625 .0152916
occ7 | -.0315213 .0062851 -.0378064 .0151647
occ8 | -.0582498 -.0704941 .0122443 .0296871
------------------------------------------------------------------------------
b = consistent under Ho and Ha; obtained from xtreg
B = inconsistent under Ha, efficient under Ho; obtained from xtreg
Test: Ho: difference in coefficients not systematic
chi2(17) = (b-B)'[(V_b-V_B)^(-1)](b-B)
= 54.57
Prob>chi2 = 0.0000
(V_b-V_B is not positive definite)
ハウスマン検定の結果,変量効果モデルの推定値が固定効果モデルと異ならないという帰無仮説が棄却されたので,最終的に固定効果モデルが採用された.
問題:data_st_divorce.dtaは,ある年に調査された離婚についてデータである.このデータを使って,以下の問題に答えよ,なお,データセットにある各変数は,以下のとおりである.
(1) 離婚までの月数のメディアンを学歴ごとに調べよ.
生存時間分析を行う場合,最初にデータセットが生存時間分析のデータであることをstsetコマンドで宣言する.このデータでは時生存間の変数はdur,イベント経験の変数はdiv,個体を識別する変数はnoであるから,stset コマンドを次のように入力する.
. stset dur, failure(div==1) id(no)
id: no
failure event: div == 1
obs. time interval: (dur[_n-1], dur]
exit on or before: failure
------------------------------------------------------------------------------
1310 total obs.
0 exclusions
------------------------------------------------------------------------------
1310 obs. remaining, representing
1310 subjects
908 failures in single failure-per-subject data
27114 total analysis time at risk, at risk from t = 0
earliest observed entry t = 0
last observed exit t = 60
生存時間の記述統計を出力させるにはstsumコマンドを用いる.さらに,byをオプションで付けて学歴グループごとのメディアンを計算することを指定する.
. stsum, by(edu)
failure _d: div == 1
analysis time _t: dur
id: no
| incidence no. of |------ Survival time -----|
edu | time at risk rate subjects 25% 50% 75%
---------+---------------------------------------------------------------------
high sch | 12597 .0468365 601 12 20 28
universi | 14517 .0219054 709 17 29 43
---------+---------------------------------------------------------------------
total | 27114 .0334882 1310 14 23 34
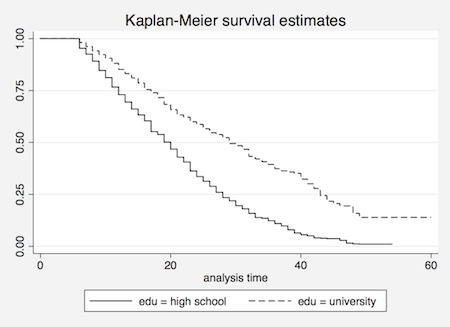
出力結果を見ると,高校卒のメディアンは20ヶ月,大学卒では29ヶ月である.したがって,高校卒の人は大学卒の人と比べて,結婚後かなり早いテンポで離婚を経験している.
(2) カプラン・マイヤー法による生存関数のグラフを学歴グループごとに示せ.
生存関数のグラフを出力させるには,sts graphコマンドを用いる.学歴別のグラフにするのはbyをオプションで付ける.
sts graph, by(edu)
(3) 離婚までの年数に学歴グループ間で差があるかログランク検定と一般化ウイルコクソン検定で検討せよ.
ログランク検定は
. sts test edu
failure _d: div == 1
analysis time _t: dur
id: no
Log-rank test for equality of survivor functions
| Events Events
edu | observed expected
------------+-------------------------
high school | 590 425.63
university | 318 482.37
------------+-------------------------
Total | 908 908.00
chi2(1) = 125.97
Pr>chi2 = 0.0000
一般化ウイルコクソン検定は
. sts test edu, wilcoxon
failure _d: div == 1
analysis time _t: dur
id: no
Wilcoxon (Breslow) test for equality of survivor functions
| Events Events Sum of
edu | observed expected ranks
------------+--------------------------------------
high school | 590 425.63 104468
university | 318 482.37 -104468
------------+--------------------------------------
Total | 908 908.00 0
chi2(1) = 82.03
Pr>chi2 = 0.0000
(4) 離婚までの期間について,学歴と結婚年齢の影響をCox比例ハザードモデルで分析せよ.
Cox比例ハザードモデルにはstcoxコマンドを使う.このコマンドの後に共変量(独立変数)指定する.
. stcox edu mage
failure _d: div == 1
analysis time _t: dur
id: no
Iteration 0: log likelihood = -5692.2712
Iteration 1: log likelihood = -5595.0788
Iteration 2: log likelihood = -5592.4619
Iteration 3: log likelihood = -5592.4586
Refining estimates:
Iteration 0: log likelihood = -5592.4586
Cox regression -- Breslow method for ties
No. of subjects = 1310 Number of obs = 1310
No. of failures = 908
Time at risk = 27114
LR chi2(2) = 199.63
Log likelihood = -5592.4586 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
_t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
edu | .3436498 .0283812 -12.93 0.000 .2922923 .4040312
mage | .918936 .0087969 -8.83 0.000 .9018551 .9363403
------------------------------------------------------------------------------
出力結果では,学歴も結婚年齢もともに有意な効果を示している.大学卒の離婚のハザード率は高校卒の35%になっており,結婚年齢が一歳上昇するとハザード率は10%低下し90%になる.