計算と誤差
TOPに戻る
１）計算後の処理
数値解析でもっとも重要なことは、プログラムを作って計算することではない。その結果が正しいかを判断し、その結果を使って何かを実行することが重要である。まず、プログラムが正しいかどうかの検討が必要である。そのためには、正解がわかっているデータに対して、正しい答えが出るかのチェックをすればよい。あるいは、現象がわかっているデータに対して、その現象を数値的に再現できるかどうか。そして、誤差はどれだけか。いろんなデータに対してチェックすることが必要である。
答の可視化も重要である。目で見てわかるような振動波形など、グラフ化して示すことも重要な処理の一つである。
２）誤差
ある入力データに対して、数値シミュレーションをした結果と、真の値との差を誤差という。コンピュータは絶対計算を間違えないと普通の人は思う。正常な条件のもとでは計算を正確に繰り返す。しかし、コンピュータにもいろいろな誤差が入り込む原因があり、この誤差も正確に繰り返される。計算機特有の誤差について説明する。
（２−１） 入力データの誤差
入力する段階ですでに存在している誤差をいう。公式中の1/3とか、√2とか、e、πなどを有限小数で表現するための誤差である。xに１％の誤差があると、xの２乗には1.01×1.01=1.0201と２％の誤差が生じる。このように、誤差が次の計算に次々と伝わっていくことをと誤差の伝播という。
（２−２） 丸め誤差
コンピュータは、10進数を2進数になおして記憶する。このとき、小数点以下を含む10進数は、2進数に変換される時に変換誤差を生ずる。これが丸め誤差という。
10進数の5は、2進数では
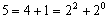だから101である。このように整数には変換誤差はない。また、10進数の0.875は、
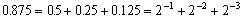であり、2進数では0.111となって変換誤差はない。しかし、10進数の0.6は、
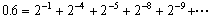であり、2進数では0.100110011...となる。ここで１個の数値を８ビットで表わすものとすると、0.10011001となり、それより下位の桁は切り捨てられてしまう。
逆にこれを10進数に戻すと、
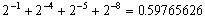となって、元の値0.6との間に差が生じる。これが丸め誤差である。0.6を変数に代入して、すぐ取り出すだけでもう誤差が生じる。
次に、丸め誤差の伝播について。簡単のため、有効数字2桁しか記憶できないコンピュータを考える。0.12345は、切り捨てられて0.12となる。実際には2進数で記憶する際には、さらに変換誤差が加わる。
また、３つの数の足し算では、
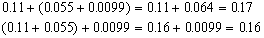
となって、答えが違ってくる。
実際のコンピュータでも、有効数字２桁ということはないが、有効数字８桁程度。このように、コンピュータの制限のために、演算のたびに毎回丸め誤差を発生し、計算が進むに従って誤差が伝播していく。また、この例のように、計算の正確さは計算順序にも依存する。コンピュータの小数演算では、数学における交換法則、結合法則、分配法則は必ずしも成立しない。
今度は、計算がいくつかの段階に分かれていて、前の段階の値を使って次の段階の答えを求める場合の、誤差の伝播について考えてみる。
漸化式
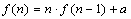
前の値のn倍にaを加える。前の誤差もn倍されてしまい、計算が進むにつれて誤差もどんどん大きくなる。しまいには真の値より誤差の方が大きくなってしまう。逆に、十分大きなnの値から、nを下げる方向に計算していけば、誤差も1/nずつ小さくなっていき、誤差の拡大を防ぐことができる。このように、計算の仕方を工夫することによって、誤差を小さくすることも、数値計算では重要なことである。
では、丸め誤差を使って計算機をだましてみよう。
新しく、gosa1 というファイルを作成する。
Sub gosa1()
Dim a, b As Double
a = 0.6
b = 3 * a
Worksheets("Sheet2").Cells(1, 1).Value = b
If b = 1.8 Then
Worksheets("Sheet2").Cells(1, 2).Value = "same"
Else
Worksheets("Sheet2").Cells(1, 2).Value = "different"
End If
End Sub
このプログラムは、b = 3 * 0.6 = 1.8を計算し、それを画面に表示させている。
そのあとで、bが1.8と等しいかどうかを判断させ、等しければsame、
違っていればdifferentと表示させるというものである。
ファイルを保存して実行してみる。
1.8と表示しておきながら、1.8とは違う(different)と表示することと思う。
このように、条件判断で実数の比較をさせると、思わぬエラーが出ることがある。
（２−３） 打ち切り誤差
処理に用いられる計算式が近似式であるために発生する。無限級数を有限の項で近似する場合など。例えば、台形公式で定積分を計算する場合、分割数nを大きくしていけば、近似の度合いを増すことができ、打ち切り誤差を小さくすることができる。しかし、分割数を大きくしすぎると、今度は丸め誤差が大きくなってかえって変な値になってしまう。細かくすればよいというものでもない。
（２−４） 桁落ち誤差
有効数字のうち、大きい方がそろっている２つの数を引いてしまうと、結果の有効数字が極端に少なくなる。たとえば、9.87654-9.87621=0.00033のように、有効数字６桁から２桁になってしまう。この数がかけ算などに出てくると、全体の誤差が増大してしまう。これが桁落ち誤差である。
桁落ち誤差を防ぐためには、近い数の引き算はなるべくしないよう、計算を工夫する必要がある。
例え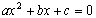ば、
の解は、
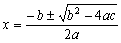
となるが、これは、
b >0, b2 ≫ 4ac
のときに、
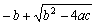の計算には桁落ちが生じやすい。この場合、分子分母に
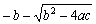をかけて式変形をして、
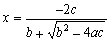で計算する。これで桁落ちの原因となる引き算を避けることができる。
実際に確かめてみよう。
新しく、 gosa2 というファイルを作成する。
Sub gosa2()
Dim a, b, c, x1, x2 As Double
a = 0.00000001
b = 100000000#
c = 0.00000001
x1 = (-b + (b * b - 4 * a * c) ^ 0.5) / 2 / a
x2 = -2 * c / (b + (b * b - 4 * a * c) ^ 0.5)
Worksheets("Sheet3").Cells(1, 1).Value = "x1="
Worksheets("Sheet3").Cells(1, 2).Value = x1
Worksheets("Sheet3").Cells(2, 1).Value = "x2="
Worksheets("Sheet3").Cells(2, 2).Value = x2
End Sub
このプログラムは、a=1e-8（10の-8乗）、b=1e+8（10の+8乗）、c=1e-8（10の-8乗）の
場合に、普通に解いた時の解をx1に、式変形をして解いたときの解をx2に入れ、
それぞれ表示させるものである。 ファイルを保存して実行してみる。
理論的には、どちらも同じ数となるはずだが、実際にはx1が０になってしまい、
x2と異なった値が表示されることと思う。
このように、結果が桁落ちしている場合には気づきやすいが、
計算の途中で用いられる値が桁落ちしている場合には、なかなか気づきにくいので、
注意を要する。
３）計算結果の検討
これらの誤差のために、コンピュータによって出力された計算結果の数字が
どこまで有効であるか、見極めるのが重要。
真の値が前もってわからない場合には、データを少し替えてみたり、
異なった誤差を持つ近似式に替えてみたり、演算順序を変更したりして、
満足のいく結果に到達させていく。
（３−１） デバッグ
プログラムのどこかに間違いがあって結果が正しくない時には、
- エディタでプログラムを修正
- 修正したプログラムを保存
- コンパイルして機械語に変換
- プログラムを実行して確認
という作業を繰り返す。
このようにしてプログラムの間違いを修正していく作業を、デバッグ（debug）という。
これは、間違いがあるのはプログラムに虫（bug）が入っているからだという比喩で、
虫を取り除く作業ということでdebugと呼んでいる。
プログラムの間違いには、文法的な間違い（syntax error）と、 実行された時に不具合が発生する場合（run-time
error）などがある。 これらの間違いには、コンピュータがメッセージ（error
message）を表示するので、 必ず読むこと。 たいていは英語で書かれているが、簡単な英語なのでちゃんと読むように。
ただし、使う式やアルゴリズムが間違っているという論理的な間違いは見つけてくれない。
ちゃんと答が表示されてもその値が違っている時には、どこがおかしいのか、
人間が一生懸命考えて間違いを探す必要がある。
（３−２） 整数と実数
よく間違いやすい問題に、整数と実数の違いがある。
人間にとっては、1も1.0も同じ数だが、コンピュータは整数の1と実数の1.0とを区別する。
整数と実数は記憶の方法が違うからである。
TOPに戻る