エクセルの活用(4)
～ 関数のプロット ～

1. 相対参照と絶対参照

　関数のグラフを描くにあたって，セルの相対参照と絶対参照についてしっかり理解しておく必要がある．下のリンクを左クリックしてファイルを保存（または右クリックし「名前をつけてリンク先を保存」を選択）する．今日使うエクセルシート function.xlsx を各自で用意したUSBメモリに保存する．

function.xlsx

　保存したらダブルクリックしてファイルをエクセルで開く．このファイルには3枚のシートが入っているが，その中の「練習用シート」を選ぶ．

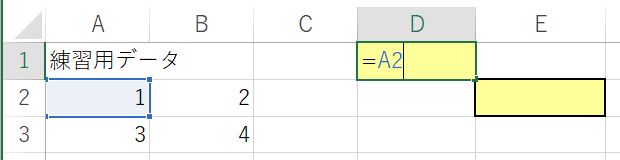
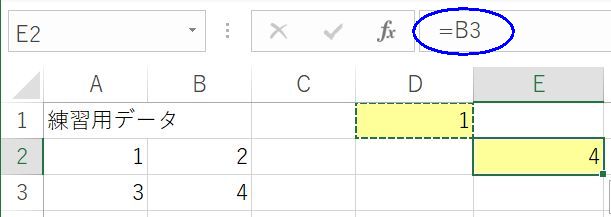
　このシートのA2～B3セルには，1，2，3，4と入力されている．黄色く塗られたD1セルに「=A2」とすると，A2セルに入っている1という数字がD1セルにも表示される．ここでD1セルをマウスで選択してコピー（Ctrl+C）し，もう一つ黄色く塗られたE2セルに貼りつけると（Ctrl+V），4と表示されたと思う．なぜ4になったか考えよう．貼りつけたE2セルの式を確認すると，「=B3」となっている．「=A2」という式をコピーして貼り付けると，自動的に「=B3」に変化したということ．これが表計算ソフト特有の相対参照と呼ばれる機能である．D1セルに入力した「=A2」という式は，今いる場所から3つ左で，1つ下という相対的な位置にあるセルの値を参照するという意味になる．だからE2セルにその式を貼りつけると，E2セルから3つ左で，1つ下にあるB3セルを参照したということである．

相対参照

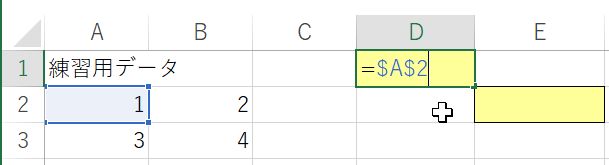
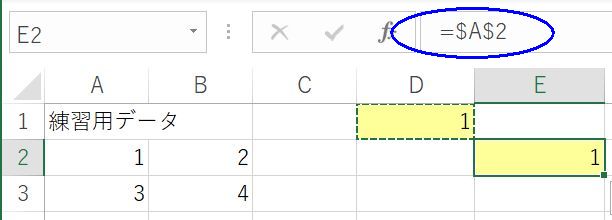
　相対参照は自動的に参照場所が変わるので便利なのだが，時には参照場所を変えたくないことがある．そんなときには，相対参照ではなく絶対参照をすればよい．一度D1～E2セルを選んで「DELETEキー」を押して内容を消し，もう一度D1セルに式を入力しよう．今度は「=A2」と入力した後に「F4キー」を押す．すると式が「=$A$2」に変化する．このD1セルをコピーして，E2セルに貼りつけてほしい．すると表示される値は1になる．E2セルの式を確認すると「=$A$2」となっていると思う．$が付くと場所を変えてコピー＆ペーストしても，参照するセルが変化しない．

絶対参照

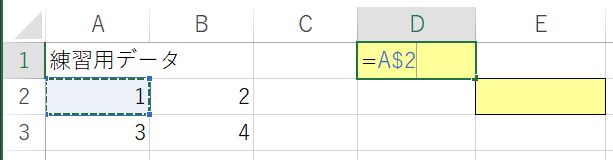
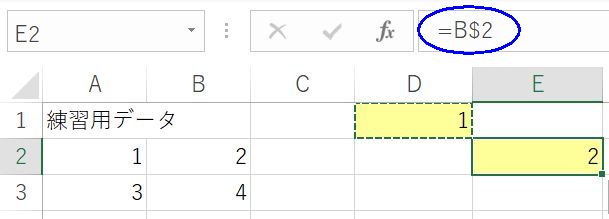
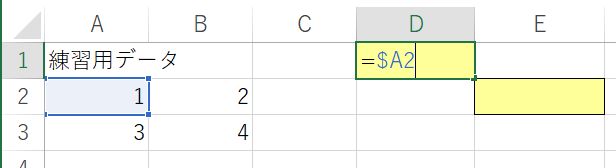
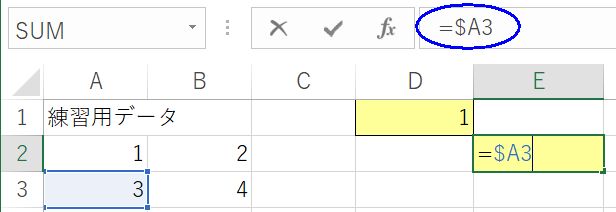
　この絶対参照は，列だけとか行だけも可能である．一度D1～E2セルの内容を消して，もう一度D1セルに式を入力しよう．「=A2」と入力した後「F4キー」を何度か押してほしい．A2→$A$2→A$2→$A2→A2と順番に変化する．A$2は2行目という行だけ絶対参照し，$A2はA列という列だけ絶対参照することになる．「=A$2」となったところでEnterキーを押し，D1セルをコピーしてE2セルに貼りつけよう．すると，値が2となる．式は「=B$2」とAがBに変化し，2行目を意味する2は変化していない．これが行だけ絶対参照するという意味である．再度D1～E2セルの内容を消して，D1セルを「=$A2」としてE2セルにコピー＆ペーストすると，今度は3と表示される．式を確認すると「=$A3」となっていて，A列は変化していないが2が3に変化している．これが列だけ絶対参照するということである．

行の絶対参照
列の絶対参照

　このように，後でコピー＆ペーストした時，変化してほしい行や列は相対参照にし，変化してほしくない行や列は$を付けて絶対参照するのが，エクセルを使いこなすコツ．思わぬセルを参照してしまわないよう，コピー＆ペーストや連続コピーをした時には十分注意する必要がある．

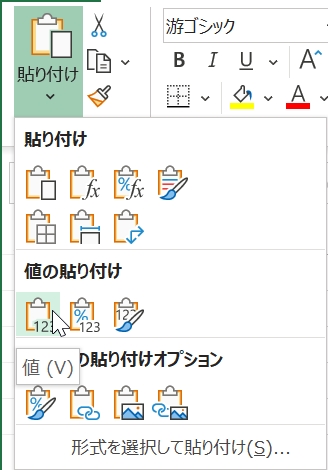
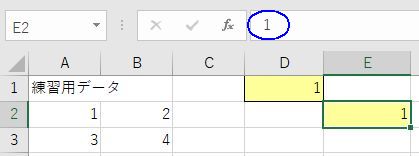
　最後に「値として貼り付け」も演習しておこう．式ではなく値をコピー＆ペーストしたいときに使う．再度D1～E2セルの内容を消し，もう一度D1セルに「=A2」と入力しよう．D1セルをコピーした後，E2セルをクリックしてアクティブにする．左上の「貼りつけ」の下矢印を押して出てくるメニューから「値の貼りつけ」の一番左，「123」と書かれているボタンを押すと，D1セルの内容が数値としてコピーされる．式を確認すると「1」という数字だけになっていると思う．

値として貼り付け

2. 関数のグラフ

　では，関数をプロットする練習をする．例題として，ばねについたおもりの自由振動の様子を描くことにする．

　ばね定数を\(k\)，おもりの質量を\(m\)，ばねの自然な状態から最初に伸ばした量をx_iniとすると，ばねの自由振動の様子（ばねの伸び縮みする様子）は次の式で表現できる．

　y = x_ini * cos(\(\omega t\))

y は \(t\) 秒後のばねの位置（ばねの自然な状態での位置からの距離で変位という），\(\omega\)は角速度で \(\omega = \sqrt{k/m}\) である．

　ばね定数 \(k\) = 10 N/m，質量 \(m\) = 10 kg，初期変位 x_ini = 1 mの場合，この関数をグラフ化してみよう．「関数プロット」というシートを選択する．

(1) パラメータの入力

　B1セルに\(k\)の値として10を，B2セルに\(m\)の値として10を，B3セルにx_iniの値として1を入力する．次に\(\omega\)を計算する．セルB4に数式「=sqrt(B1/B2)」を入力する(図1)．sqrt()はルートを計算する関数．

図1		図2

(2) 式の入力

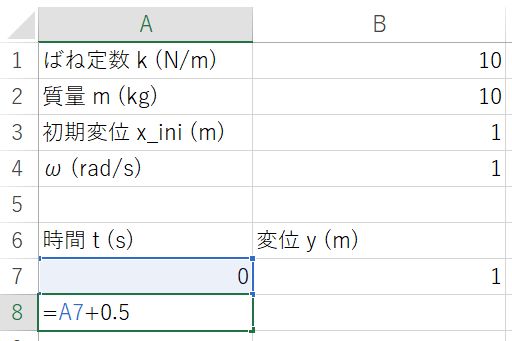
　A列に時間t，B列に変位 y の値を入力していく．A7セルには初期時間\(t=0\)ということで0が入っている．B7セルに変位の初期値としてx_iniの値が入っているセルB3を参照する式「=B3」を入力する（図2）．

　では，時間の列を完成させよう．計算する時間間隔を0.5秒とし，先ほど入力したセルA7の値に0.5を足す式をA8に入力する．これは，A8に「=A7+0.5」と入力することによってできる（図3）．このA8に入力した数式を必要な時間が得られるまで下方向にコピーすれば良い．ここでは，30秒後まで表示できるようにしておくため，A67セルまでコピー＆ペーストしよう．A8セルを選択した状態でマウスのホイールを回しA67セルを表示させる．Shiftキーを押したままA67セルをマウス左ボタンでクリックすると，A8～A67セルが選択された状態になる．選択された状態のまま，Ctrl+Dを押すと30まで0.5刻みの時間軸が完成する．

　次に変位の列を完成させる．B8セルに「=B$3*cos(B$4*$A8)」と入力する（図4）．先ほど演習したセルの相対参照と絶対参照をよく考えること．あとでコピー＆ペーストしたときに，B列の値は行番号が変わったら変な計算になるので，行の絶対参照にしておく．B列という列を絶対参照にしないのは，後でパラメータを変えた値をC列で計算するためである．A8を$A8と列の絶対参照にするのも同じ理由．このように，後でどこにコピー＆ペーストするかを考えて，相対参照と絶対参照を使い分けると便利だが，実際には最初からそんなにうまくいかなことが多い．コピー＆ペーストした結果がおかしかったら，その時点で相対参照と絶対参照を修正すればよい．B8に入力された数式を下方向にコピーしてB列の値を完成させる．B8セルを選択し，B8セル右下に表示されるフィルハンドルをダブルクリックすればよい．

図3	図4

(3) グラフ化

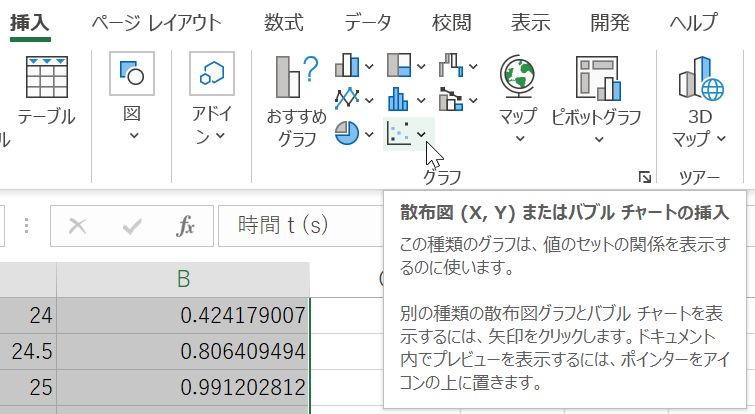
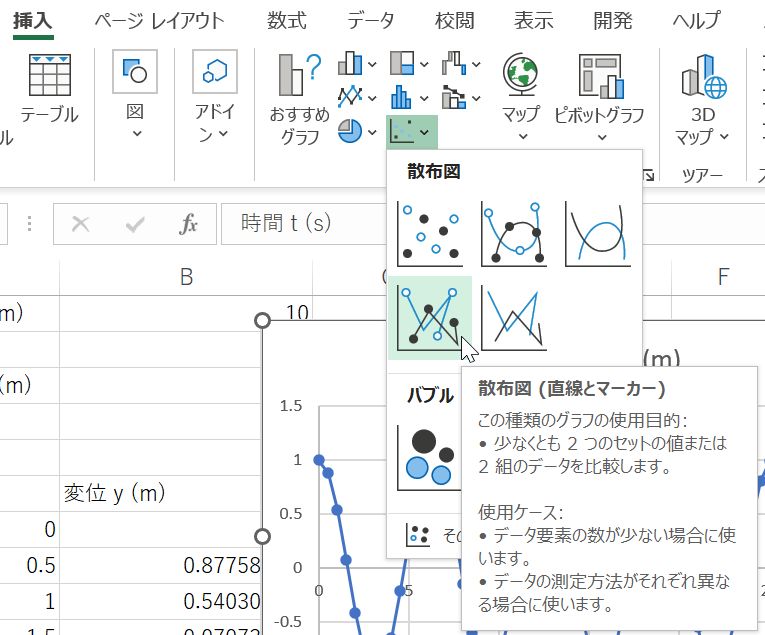
　完成したA列とB列の値をグラフ化する．A6～B67セル（列の説明があるセルから数字の最後のセルまで）を選択し，挿入メニューのグラフ欄から「散布図（X，Y）またはバブルチャートの挿入」を選び（図5），表示された何種類かのグラフから「散布図（直線とマーカー）」を選ぶ（図6）．連続したセルを効率的に選択するには，左上のセルを選んだ状態でShiftキー＋Ctrlキー＋下向き矢印，さらにShiftキーとCtrlキーを抑えたまま右向き矢印を押すという方法もある．Shiftキーには選択し続けるという機能があり，Ctrlキー＋矢印キーで連続したセルの端まで移動するという機能がある．もちろんマウスの左ボタンを押しながらマウスポインターを移動させるドラッグという機能を使っても構わない．

図5	図6

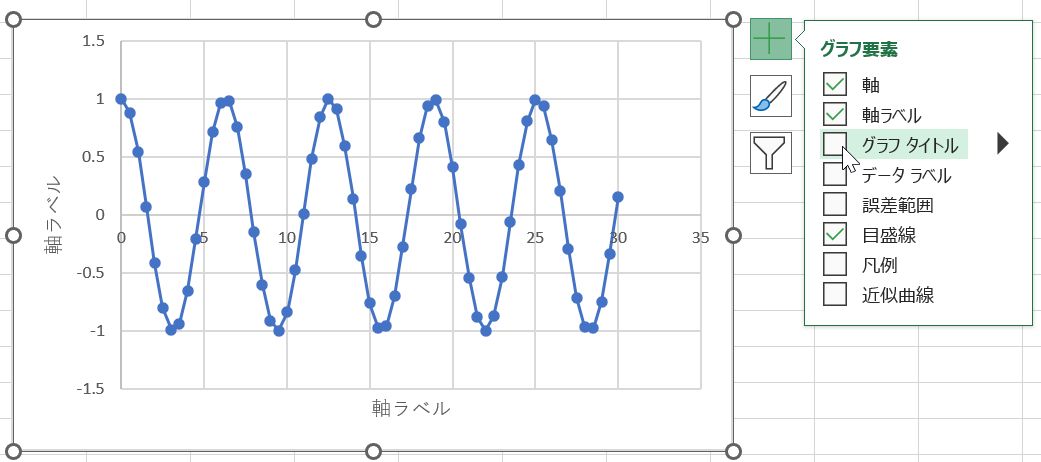
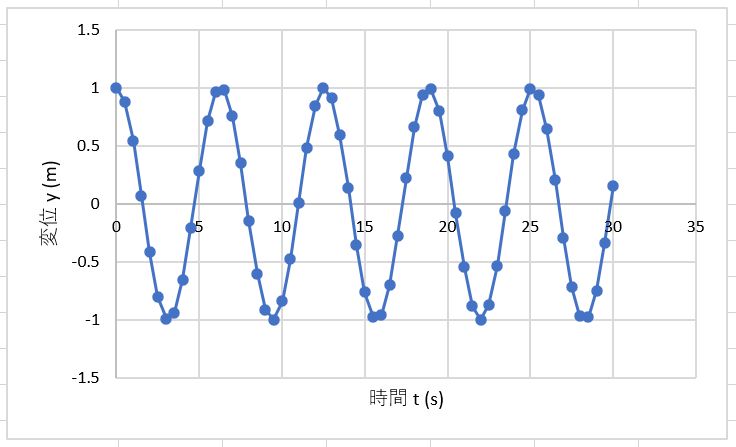
　あとは，これまでと同じように，軸ラベルを追加し，グラフタイトルを消しておく．グラフを選択したら右上に表示される「＋」をクリックし，「軸ラベル」をチェックし「タイトル」のチェックを外す（図7）．軸ラベルは，横軸を「時間t (s)」，縦軸を「変位y (m)」とする．横軸の軸ラベルをクリックして「=A6」，縦軸の軸ラベルをクリックして「=B6」とするか，軸ラベルをダブルクリックしてキーボードから入力するか，どちらの方法でもよい．これで，振動する物体の変位が時間によって変化するグラフ（時刻歴波形）が表示された（図8）．図8のようにならなければ，どこかに間違いがあるので式を見直そう．

図7	図8

(4) 2つの波形の表示

　レポートなどでは，二つの条件で得られたデータを比較することがある（というか，多い）．そこで，おもりの質量を2倍の20kgにした時のグラフもプロットし，比較してみることにする．

　まず，C列に，ばね定数 \(k\) = 10 N/m，質量 \(m\) = 20 kg，初期変位 x_ini = 1 m の値を入力し，\(\omega\)の式もB4セルからC4セルにコピーしておく．さらにB7～B67セルを選択し，右下のフィルハンドルをクリックして右のC列まで動かし，C7～C67セルにコピーする．

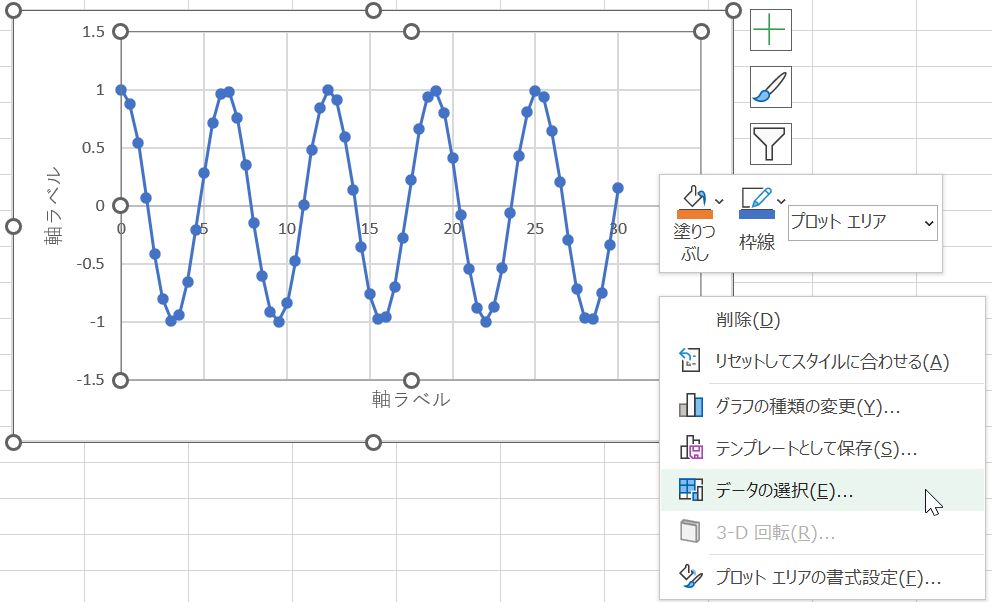
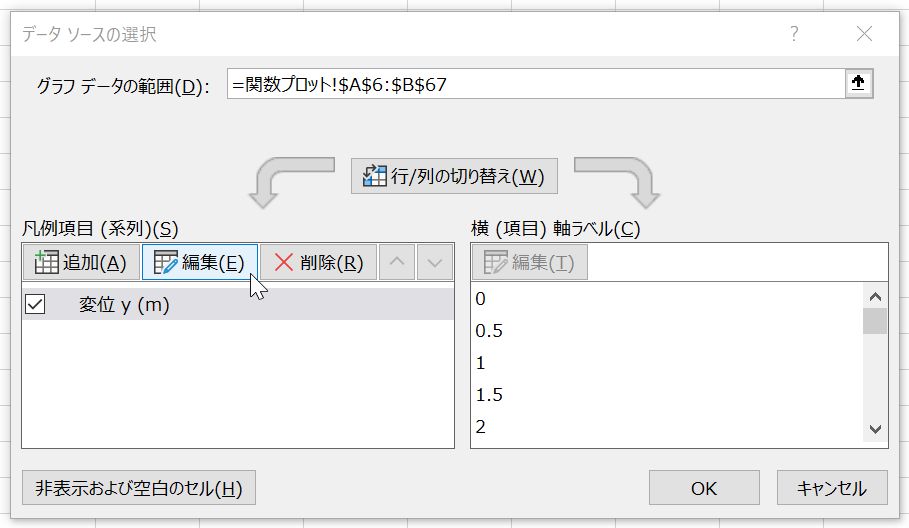
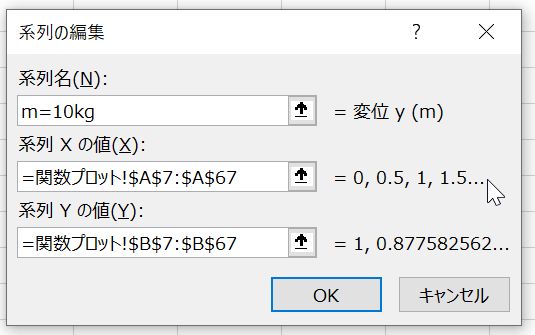
　次に新しく追加したC7～C67セルのデータをグラフに追加する．グラフを選択して右クリック，表示されるメニューから「データの選択」を選択する(図9)．現れた「データソースの選択」ウィンドウに表示されている「変位y (m)」を選んで編集ボタンを押す(図10)．「系列名」を「m=10kg」に変更して「OK」ボタンを押す(図11)．

図9	図10	図11

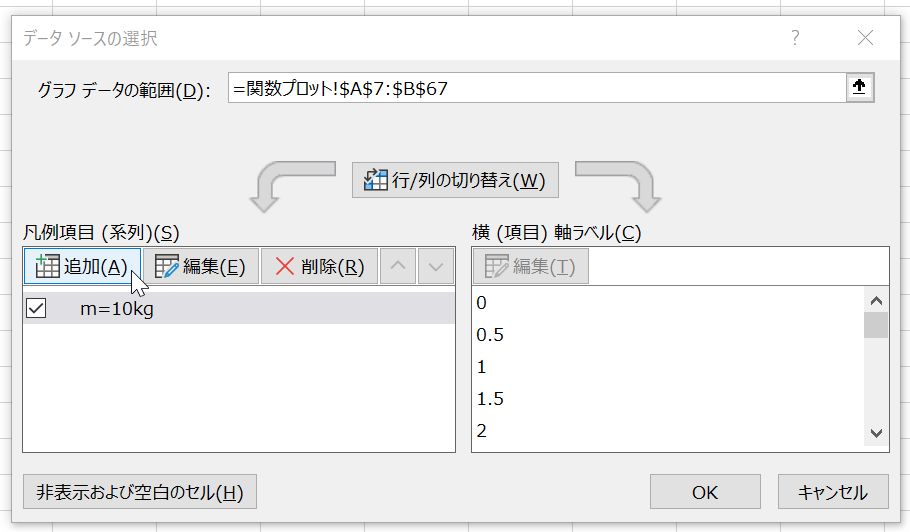
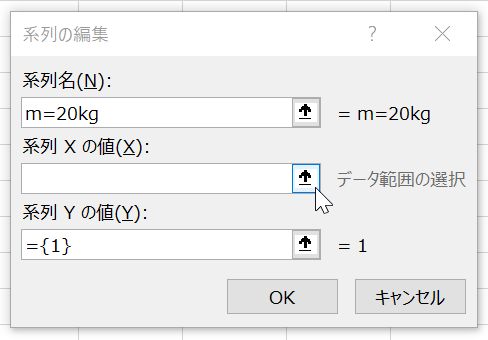
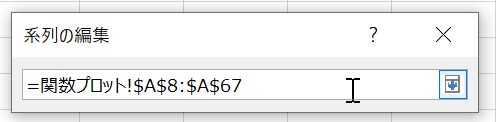
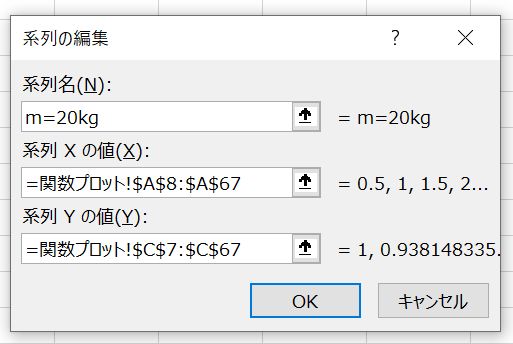
　次に「データソースの選択」ウィンドウの「追加」タブをクリックすると（図12），「系列の編集」ウィンドウが現れる（図13）．「系列名」に「m=20kg」と入力する．「系列Xの値」のテキストボックスの右端にあるマークをクリックし，データのあるA7～A67の範囲を選択してEnterキーを押す．「系列Yの値」のテキストボックスの右端にあるマークをクリックし，データのあるC7～C67の範囲を選択してEnterキーを押す．選択が終わったら最後に「OK」をクリックし（図14），「系列の編集」→「データソースの選択」ウィンドウを閉じる．同じグラフ上に2つのデータが色違いで表示されていると思う．

図12	図13	図14

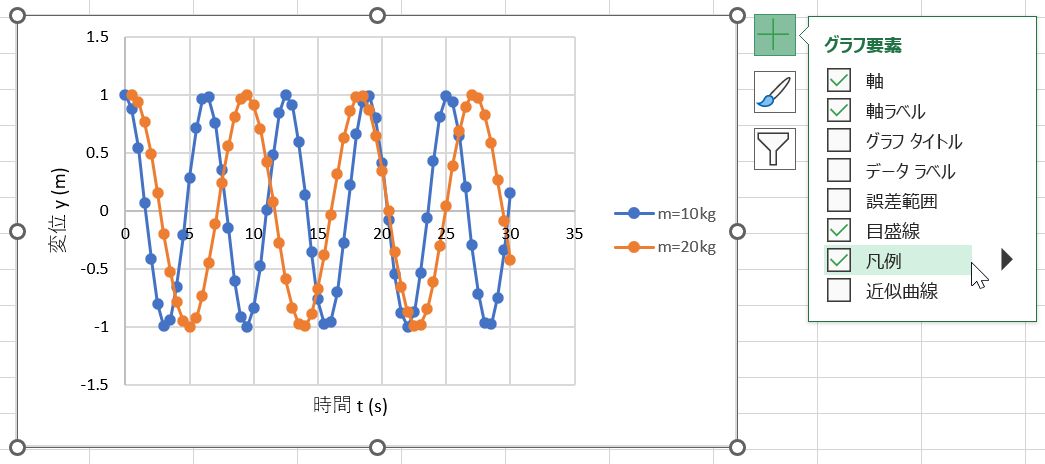
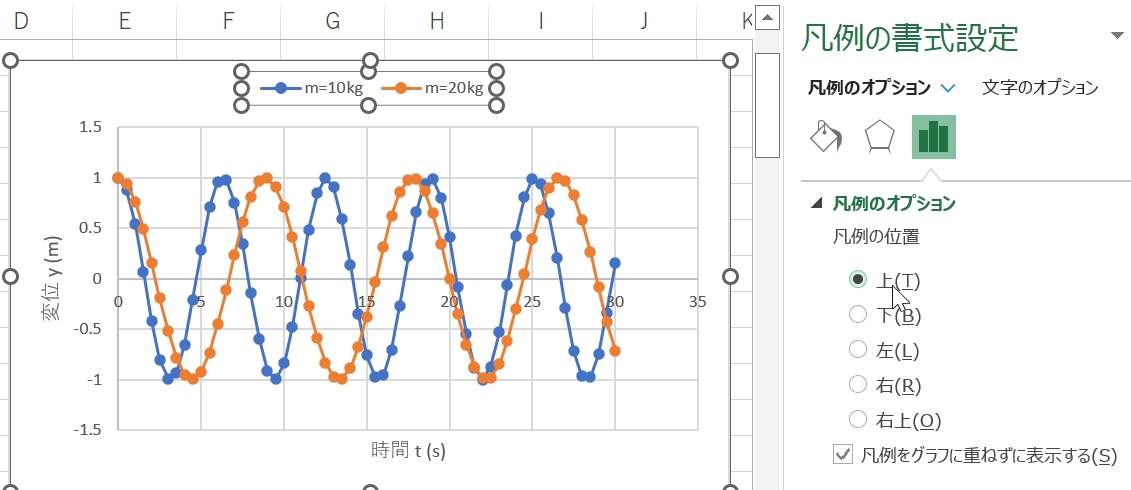
　これで，ばねで揺れる2つの物体の時刻歴波形ができたが，どっちの線が何を表しているのかという説明（凡例：はんれい）がないのでわからない．グラフをクリックまたはダブルクリックして表示される「＋」をクリックすると，グラフ要素のメニューが現れる，凡例にチェックを入れると（図15），系列名に入力したm=10kgとm=20kgがグラフの右に表示されるはず．凡例の位置を変えるには，凡例をクリックして右に表示される「凡例の書式設定」メニューで，凡例の位置を「上」にチェックする（図16）．

図15	図16

　今回作ったグラフを眺めてみよう．質量が異なることによって，グラフにどんな変化が現れたかな？質量の影響は予想通りか考えてみよう．このようにエクセルでは色々な関数を表現でき，さらにグラフ上にプロットすることができる．今回の例のように，条件の異なる結果をグラフ化して比較することは非常に役に立つ「技術」である．これからも役に立つと思うのでしっかり身につけておこう．

3. 補足：グラフをきれいに

　作ったグラフは，線と横軸とが重なっていてわかりにくいし，グラフの右が35秒まであって少し変．横軸をダブルクリックすると，右に「軸の書式設定」メニューが現れる．「軸のオプション」（表示されてなければ棒グラフの絵をクリック）の最大値を35.0から30に変更．メニューの下の方にある「ラベル」を「軸の下/左」から「下端/左端」に変更（図17）．軸ラベルや値の色が灰色になっているので，クリックして色を黒に変更．これでかなり見やすくなると思う（図18）．他にも線をクリックして線の色を好きな色に変えるとか，いろいろ試してみよう．エクセルが自動で描画するグラフは主にビジネス分野で使われるグラフが多く，ディスプレイで見るときれいでも印刷するとわかりにくい場合が多い．工学系で使われるグラフには，見た目のきれいさよりも違いがしっかりとわかることが求められるので，黄色い線や小さな文字など，見にくい表現はしないよう注意しよう．

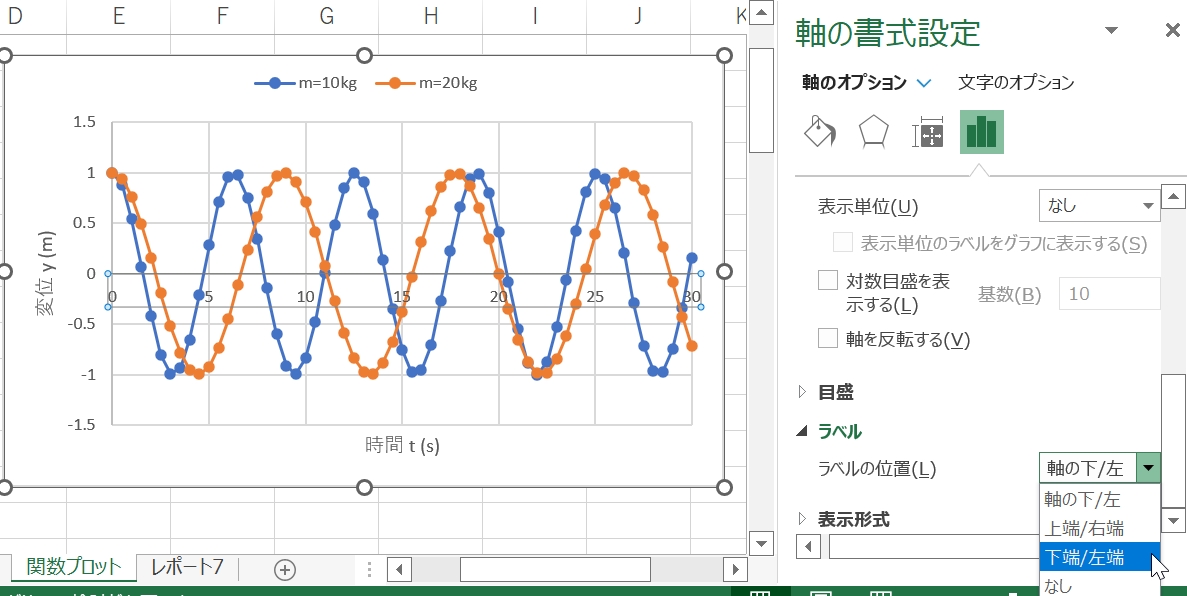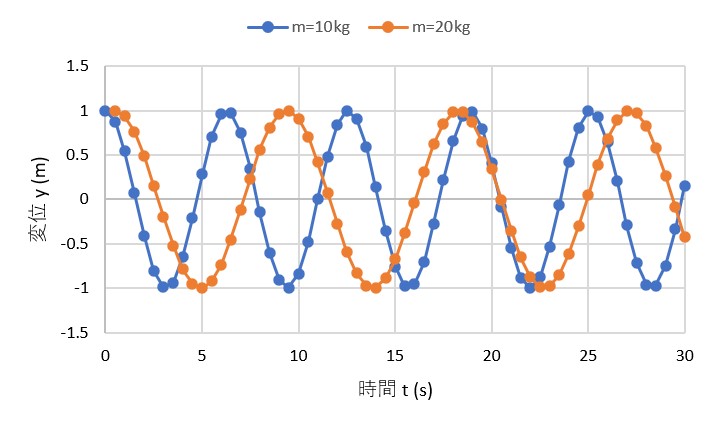図17	図18