● フーリエ解析
フーリエ解析については応用数学で習っているはずなので、復習程度の説明で済ませます。
時間の座標上で現れている現象を周波数の座標で表現するものがフーリエ級数およびフーリエ積分です。時間と周波数は一対一の関係が有り、時間特性として特徴付けられるものは全て周波数特性で特徴付けられます。また、線形システムの場合、時間応答よりも周波数応答の方がそのシステムを特徴付け易くなります。
ここでは線形拡散方程式を対象にフーリエ展開を施し、その時間特性と周波数特性を明らかにしてみましょう。
● フーリエ解析の復習
ある関数f(x)がある区間[0,T]で連続であり、且つ積分可能な場合
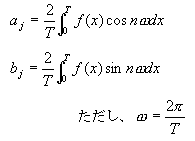
を関数f(x)のフーリエ係数と呼び、この時f(x)は形式的な級数
![]()
で表すことが出来ます。この級数をフーリエ級数といいます。実際には無限大まで解析するわけにはいかないので、どこかで切断する必要があります。上式で有限な項までで解析を行うことをフーリエ解析と呼んでいます。