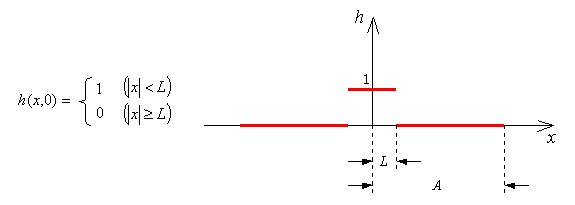
では実際に、線形拡散方程式にフーリエ解析を利用してみましょう。

上記のような不連続な関数の拡散現象を考える。不連続な関数のままでは扱いにくいので、フーリエ展開を用いて連続関数で表現します。この関数に対してフーリエ展開行うと、
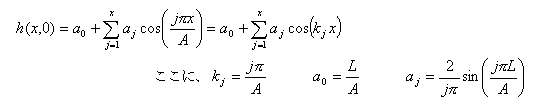
これにより、初期時刻におけるフーリエ級数を得ることが出来る。前ページで紹介した式と少々違いますが、これは関数h(x,0)
が偶関数であることを利用しています。
では、任意の時刻におけるフーリエ級数はどのようにして得られるのだろうか?初期時刻から任意の時刻に到達するまでに、拡散現象を起こしている。このことを拡散の割合を示すパラメータH(kj,t)で表現する。すると、任意の時刻におけるフーリエ級数は次のように表現できる。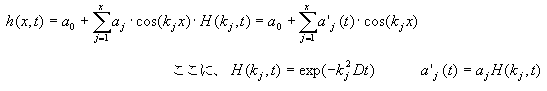
PROBLEM
![]()
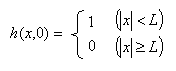
拡散問題を考える。拡散現象が左上の式によって支配されるとする。この拡散現象の初期条件が右上のように与えられる。
L=2,A=10,D=0.01の時、h(x,t)はどのように表現されるか?