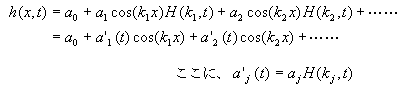
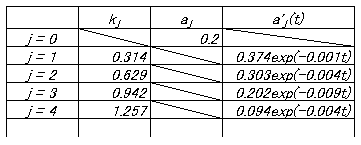
任意の時刻t=t のときの解は、フーリエ展開により次のように求められます。
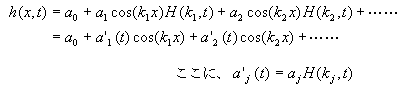

となります。皆さんも確認してみてください。これにより任意の時刻におけるフーリエ級数を求めることが可能になりました。念のために初期時刻におけるフーリエ級数は、上式においてt=0 を代入すればOKです。
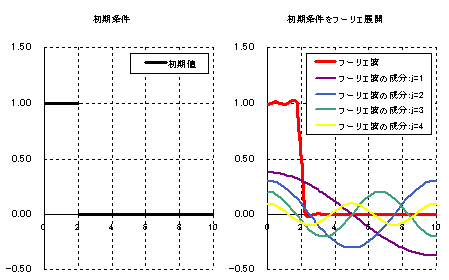
では、このh(x,t)がどのような挙動を示すか実際に見てみましょう。
下の図は、t=0〜1000までの挙動を示しています。

赤色はフーリエ級数h(x,t)を示しています。
紫色:b1cos(k1x) 青色:b2cos(k2x) 緑色:b3cos(k3x) 黄色:b4cos(k4x)
上述のANSWERと照らし合わせながら見て下さい。
どうでしたか?ちょっとゴチャゴチャしていて分かりにくいですが、赤色の波(フーリエ級数)が拡散している様子がわかったかと思います。初期状態でh(x=0,t=0)=1だった波が、時間が経つにつれてx軸の正の方向へ拡散していますね。