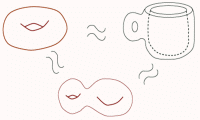Geometry is a branch of mathematics which study properties of figures (spaces). Among them, topology is a geometry which studies properties that are invariant under continuous deformations.

If we consider (the surface of) the donuts as made of rubber, we can deform it to be a shape of (the surface of) a coffee cup. Conversely, we can also deform the coffee cup to the donuts. Both of them has a common property that they have one hole, and this number of holes is invariant under the deformation of the figures like rubbers. We call such a quantity "topological invariant".

In this way, it may be allowed to say that topology is a geometry which study properties that are invariant under the continuous deformations.

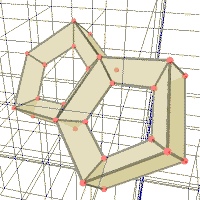What is the usefullness of topology? Let us consider for example polyhedron. Polyhedron is a figure composed of polygons glued along their edges.

A famous mathematitian L. Euler calculated the following integer.

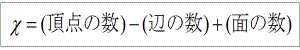
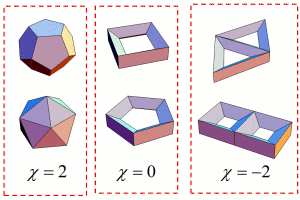
It seems amazing that he discovered such number is remarkable. The following is result of calculation of the number of the polyhedra below.

We can consider more complex figures. Euler discovered that the following formula holds.

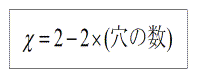
If we consider the above polyhedra as made of rubbers, we can deform these polyhedra as the following three surfaces respectively.

From this fact, we see that

(1)no matter how complex the polyhedron is, we can calculate the Euler number only by counting the number of hols without counting the number of vertices, edges, and faces.

(2)If we know the number of vertices, edges, and faces, then we can see the shape of the surfaces associated to the polyhedron.

(3)If we do not know the number of faces for example, we can calculate it from the number of vertices and edges, and holes.

If we draw edges and vertices on surfaces to regard it to be a polyhedron, we can calculate the number of holes by using the number of vertices, edges, and faces. Furthermore, this number does not chenge even if we move the surfaces continuously. We call this number topological invariant.

In this way, topology is a branch of geometry which study the property of the figures invariant under the small deformations, and it provides a srtong applications to not only analysis and algebra but also physics and engineering. For example, the argument (3) is often used to predict the existence of a solution of non-linear partial differential equations. "Solve without solve it." This is the idea of topology.

Surfaces are objects like rubber baloon which have a freedom of two directions, we can consider objects like rubber baloon which have three directions. We call these objects 3-manifolds. There are many things which we do not know very much about 3-manifolds and is studied hard now.

I am studying 3-manifold by regarding as the boundary of 4-manifolds.

We can consider the 4-manifolds as the space-time where particles are flying and fields are smeared, and we apply the idea from the theory called "gauge theory" in theoretical physics. It will be very interesting if our research will be applied to physics in turn.