演習問題(第6講)
(1)y = 12x − x3 の増減表をつくり、極値を調べよ。また、増減表を使用せずに第2階導関数を用いて極値を求めよ。
(2)y = x3 − 6x2 + 9x の増減表をつくり、極値を調べよ。また、増減表を使用せずに第2階導関数を用いて極値を求めよ。
(3)たて3cm、横8cmの長方形のブリキ板の四隅から、一辺xcmの正方形を切り取り、ふたのない容器を作る。
容器の容積ycm3を最大にするには、切り取る正方形の一辺の長さを何cmにすればよいか。
<解答>
(1) y = 12x − x3
導関数 y´= −3x2 + 12 = −3(x +
2)(x − 2)
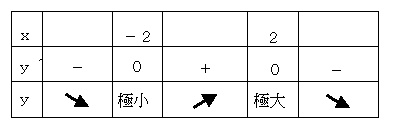
<増減表>

よって、極小値は x = −2 のとき −16
極大値は x = 2 のとき 16
<第2階導関数>
y = f(x) とする
第2階導関数 y" = −6x
x = −2 のとき y" > 0 より、接線の傾きは逓増・・・f(−2)
= −16 は極小値
x = 2 のとき y" < 0 より、接線の傾きは逓減・・・f(2)
= 16 は極大値
(2) y = x3 − 6x2 + 9x
導関数 y´= 3x2 − 12x + 9 = 3(x
− 1)(x − 3)
<増減表>
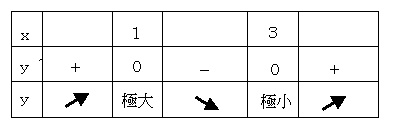
よって、極大値は x = 1 のとき 4
極小値は x = 3 のとき 0
<第2階導関数>
y = f(x) とする
第2階導関数 y" = 6x − 12 = 6(x − 2)
x = 1 のとき y" < 0 より、接線の傾きは逓減・・・f(1)
= 4 は極大値
x = 3 のとき y" > 0 より、接線の傾きは逓増・・・f(3)
= 0 は極小値
(3)容器の体積yは、
y = (3−2x)(8−2x)x = 4x3 −22x2
+ 24x (ただし、0 ≦ 2x ≦ 3、すなわち、0 ≦ x ≦ 3/2)
導関数 y´= 12x2 − 44x + 24 = 4(3x
− 2)(x − 3)
x = 2/3 と x = 3のときに極値をとる。
第2階導関数 y" = 24x − 44 = 4(6x − 11)
x = 2/3 のとき y" < 0 より、接線の傾きは逓減 x
= 2/3 のとき、極大値200/27をとる。
0 ≦ x ≦ 3/2では、常に接線の傾きは逓減しているから、極大値以上のyの値は存在しない。
よって、yを最大にするxの値は、x = 2/3 である。
#・・・すみません、定式化を間違えておりました。(小幡)