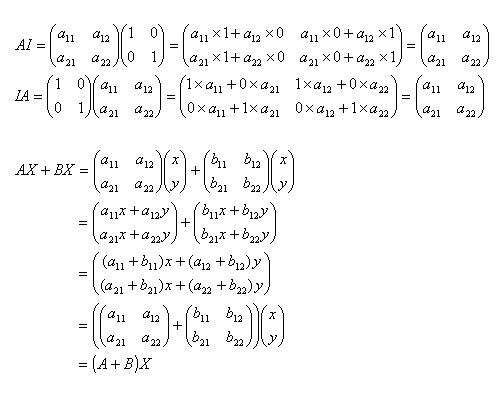
第9講 連立方程式と行列・行列式2−−−連立方程式の解法と産業連関表分析
講義の目的
1)連立方程式の解法に不可欠な逆行列と行列式の概念を理解すること。
2)逆行列を利用した連立方程式の解法を理解すること。
3)連立方程式解法の応用例としての産業連関表を理解すること。
0.行列の計算の確認
A、B:正方行列
I:単位行列
AI= IA = A (行列の積では、前後を逆にすると答えが同じならないのが通常です。)
AX + BX =(A+B)X
*証明
1.逆行列と行列式
・逆行列
AA−1 = A−1A = Iを満たす行列 A−1をAの逆行列 (Inverse)という。
例1 2行2列の正方行列
・行列式

・逆行列の求め方
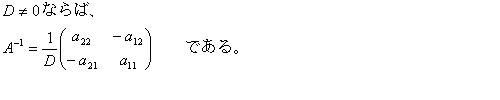
例2 2行2列を越える行列の逆行列は、EXCELなどの表計算ソフトを用いて求める。
2.逆行列を用いた連立方程式の解法
AX = B
A−1AX = A−1B
X = A−1B
例 次の連立1次方程式を、逆行列を用いて解け。
3x + 14y = 5
4x + 18y = 2
解
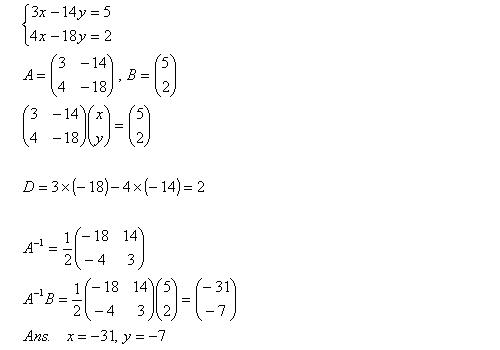
演習問題
次の連立1次方程式を、逆行列を利用して解け。
(1)3x + 2y = 4
2x + y = 1
(2)2x − 3y = 1
−x + 2y = 0
3.産業連関表分析
1)産業連関表の見方
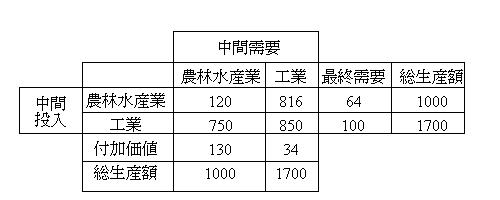
行:生産物の販路構成
農林水産業は、横方向に見ると、農林水産業に120、工業に816、最終需要として64購入されることを示す。
列:生産物の費用構成
農林水産業の生産物1000を作るために、原材料として、農林水産業から120、工業から750投入し、
賃金などを130投入したことを示す。
投入係数
産業連関表のタテに注目して、それぞれの産業の各原材料の投入額を、各々の生産額で割算して求める。
上の産連表では投入係数行列は、次のようになる。
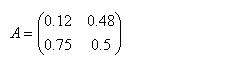
そして、総生産額(のベクトル)は、

最終需要(のベクトル)は、

そうすると、次のようになっている。
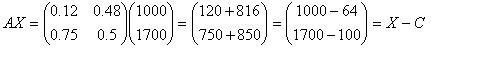
これから、X − AX = C すなわち、(I−A)X
= C
したがって、X = (I−A)−1C
これを使うと、逆に最終需要の量から総生産量を定めることができる。
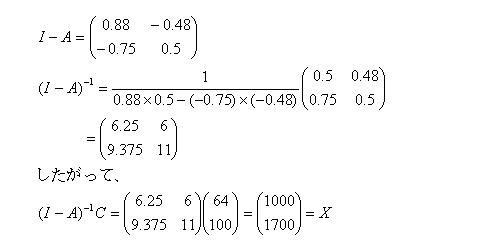
2)産業連関表の応用例−−−琵琶湖博物館の経済効果(省略)