第10講 産業連関表分析(補足)と線形計画法
講義の内容
1)線形計画法とは何か。
2)産業連関表分析の補足説明
1.線形計画法
経営科学(OR=Operations Research)
問題解決のためのオペレーションズ・リサーチ入門
高井英造/真鍋龍太郎(編著)(日本評論社)
線形計画法(LP=Linear Programming)
限られた資源を有効に配分して、目的を最大にする。
制約条件のもとで、目的関数を最大化する。
制約条件のついた最適化問題。
事例:ある工場で2つの製品A、Bを作っている。
それぞれの製品を1単位生産するのに必要な投入物は以下の通りである。
製品A: 電力20kwh 水 6トン 人 8人
製品B: 電力15kwh 水 3トン 人12人
今、一定期間に、電力は2,100kwh、水は600トン、人数はのべ1,600人使用可能とする。
また製品A及び製品Bの1単位あたりの利潤はそれぞれ40万円、25万円である。
このとき、一定期間の利潤を最大にするためには、製品A,Bをそれぞれどれだけ生産したらよいか。
生産能力のキャパシティ
定式化・・・モデル化
目的関数(利潤最大化) MAX 40x + 25y
制約条件 (電力) ST 20x + 25y ≦ 2100
(水) 6x + 3y ≦ 600
(人) 8x + 12y ≦ 1600
x>=0、y>=0
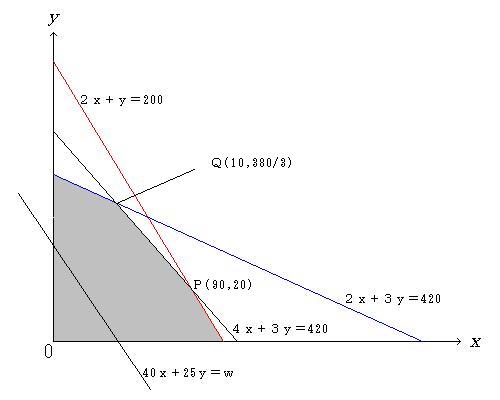
40x + 25y = w とおく。
y = −40/25x + w/25 ・・・(1)
20x + 25y ≦ 2100 4x + 3y ≦ 420
6x + 3y ≦ 600 2x + y ≦ 200
8x + 12y ≦ 1600 2x + 3y ≦ 400
y = ax+bの形になおし、x,y平面上に表す。
不等号を満たす領域が、線の上側か下側かを調べるには、
原点(0,0)を、(x,y)に代入して領域を確認するとよい。

全ての制約条件を満たす領域の中で、
(1)式のw/25を最大にする(x,y)を探す。
頂点の部分で最大値をとる可能性がある。
P点では、90×10+25×20=4100
Q点では、40×10+25×380=3566 2/3
となり、P点で最大値をとることがわかる。
ただし、製品が2つだけの場合は図解できるが、3つ以上では、図に表せない。
LPでは「シンプレックス法」などの多くの計算方法がある。
実際にはEXCELやLINDOといったコンピュータプログラムを用いて
解を求める。詳しくは「OR入門(利根川先生、2回生配当)」で。
2.産業連関表分析の補足説明
(省略)
演習問題
中間投入係数が以下のように示されている。このとき、第1財及び、第2財部門の最終需要が、
それぞれ、55、450のとき、両財の総生産高はそれぞれいくらか。
|
|
|
|
|
|
|
|
|
|
|
|
*解答は各自考えること。