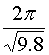最終課題(必須)
情報処理・情報処理演習の総仕上げとなる、最終課題を作成してもらいます。
課題は全部で4つあり、そのうち「演習課題1」と「演習課題2」は必須(単位取得の条件)で、
次週出題予定の「演習課題3」と「演習課題4」は任意提出ですが、提出した場合は成績にボーナス点を加えることにします。
演習課題では大まかに、
C言語によるプログラミング作成能力、gnuplotによるグラフ作成、そして LaTeX による文書作成能力の
コンピュータ技術に関する点と,報告書としてのできばえ,つまり
表現の正確さ、論理構造の正しさ,および明確さを評価します。
注 以下の力学系の記述に関しては MKS単位系を用います。
演習課題1(情報処理のレポート課題・〆切7月26日・学びステーション提出)
この問題について、以下の指示に従ったレポートを作成し、情報処理のレポート試験の答案として提出せよ。
- 表題は「常微分方程式の数値解法におけるオイラー法とルンゲ・クッタ法について」とすること。
- レポートは LaTeX で作成すること。
- 作成者の氏名、所属およびメールアドレスを表題ページに印字すること。
もしレポートを共同で作成する場合は共同執筆者全員分を表題ページに併記すること。
- レポートの構成は概ね以下のようにすること:
- (共同執筆に関する注意)共同でレポートを作成する際には、以下のことを厳守すること
- 共同執筆のグループのメンバーは概ね4名以下とし、責任者(リーダー)を一人決めること。
- 誰がレポートのどの箇所の責任をもって執筆したのかを明記すること。
- 事務にレポートを提出する際は、グループメンバーの各々が提出すること。
この際, グループの責任者がレポート正本を提出し,そのほかのメンバーは各自が担当した内容を
まとめたもの(A4一枚程度)をレポートとして提出すること.
演習課題2(情報処理演習のレポート課題・〆切7月26日・学びステーション提出)
レポート論題: ルンゲ・クッタ法による,単振り子の運動の数値解析
以下の指示に従って,プログラムのソースコード,グラフ,表を作成せよ.
質量 m のおもりを長さ l の伸びないひもに結び付けた振り子を考える。
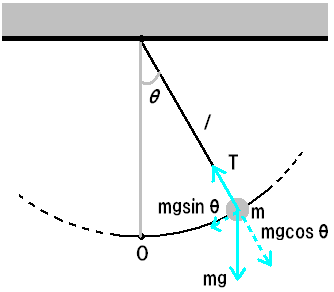
図の様に鉛直方向からの角度を Θ とおくと、運動の接線方向に着目して、運動方程式は以下のように表される
(ただし、質量 m=1、ひもの長さ l=1、重力定数 g=9.8 とおいた):
 ・・・ (式1)
・・・ (式1)
また、力学の教科書でよくやるように、十分小さな Θ については
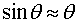
という近似を用いることで、この振り子の運動方程式は
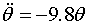 ・・・ (式2)
・・・ (式2)
のように簡単化することができる。
これらの方程式は十分小さな Θ については同じような力学系とされるが、
どの程度の Θ の大きさまでが有効な近似であるかを以下のような手法を用い調べてレポートを作成せよ。
この際、レポートは LaTeX で作成し、グラフ、表、プログラムのソースコードを含めること。
- 2つの運動方程式(式1)(式2)について、おもりを離す位置を角度(=Θ0)で与え、そこからもとの位置に戻ってくる(1周期)までの Θ をルンゲ・クッタ法で数値計算するプログラムを作成せよ。
提出物: ソースコード no.1,no.2
ヒント
「1周期の間」計算を繰り返すためには、「Θの値がΘ0に戻るまで」という条件式を for ループの条件式に書けばよい。
たとえば、『「Θ<Θ0」ただし「t=0」のときは除く』のような条件を書けばよいことになる。
- 作成したプログラムを用いて、おもりを離す位置を、Θ0=5°,10°,30°とした場合のグラフを作成し、それを印字せよ。
この際、(式1)(式2)の解のグラフは重ねて描くこと(つまりΘ0ごとに3つのグラフを作成する)。
提出物: グラフno.1,no.2,no.3
- (式1)の運動方程式について、おもりを放すときの角度 Θ0 に対して、そのときの周期 T を求めるプログラムを作成せよ。
(1. で作成したプログラムを適当に修正することでできる)
提出物: ソースコードno.3
注意
実は、Θ0の変化に対して、周期の変化は非常に小さくなっています。時間のきざみを十分に小さくしないと、正確な値がでないことがあります。
- 1°≦Θ0≦30°の範囲で、Θ0 と周期の関係のグラフを描け。
提出物: グラフ no.4
- (式2)の解の周期 Ts は(単振動なので) Θ0 に関係なく一定で
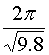
に等しい。そこで(式1)と(式2)の周期のΘ0 に関する誤差の割合
((T-Ts)/Θ0)の表およびグラフを作成せよ。
提出物: 表 no.1,グラフ no.5
TOP
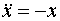

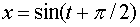

 ・・・ (式1)
・・・ (式1)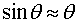
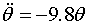 ・・・ (式2)
・・・ (式2)