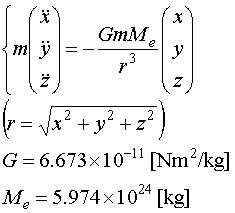最終課題(任意提出)
情報処理・情報処理演習の総仕上げとなる、最終課題を作成してもらいます。
課題は全部で4つあり、そのうち「演習課題1」と「演習課題2」は必須(単位取得の最低条件)で、
「演習課題3」と「演習課題4」は任意提出ですが、提出した場合は成績にボーナス点を加えることにします。
注 以下の力学系の記述に関しては MKS単位系を用います。
以下の演習では gnuplot の様々な機能を用いることになります。演習でやった事を用いれば完成させることができますが、
gnuplot のマニュアル
を参考にすれば、よりよい作品を作ることができるでしょう。
演習課題3(提出期限7月30日(メールでの提出を許可する))
最終課題の「演習課題2」で扱った以下の2通りの微分方程式で記述される振り子
 ・・・ (厳密な式)
・・・ (厳密な式)
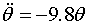 ・・・ (近似式)
・・・ (近似式)
について、これら二つの振り子を同時に動かすアニメーションを、C言語によるプログラミングとgnuplot を用いて作れ。
ただし、振り子のおもりをはなす角度Θ0については、コマンドライン引数で
与えることができるようにすること。
ちなみに、Θ0=45°の場合で、gnuplot でのアニメーションをさせる手続きの
例が
/homer/pl/tea/kht23151/Examples/gnuplot/pendsim.gpl
にあるので、参考にすること。(gnuplot の load コマンドで実行される)
演習課題4(提出期限7月30日(メールでの提出を許可する))
質量 m の物体Aと M の物体Bの間に働く万有引力は
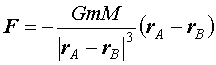
であたえられる。M が m に比べて非常に大きいときは、物体Aの運動に比較して物体Bは静止しているという近似をしてよい。
特に物体Bとして地球を考え、地球を原点にした物体Aの位置を (x,y,z) とすれば、
地球の引力に引かれる物体Aが従う微分方程式は
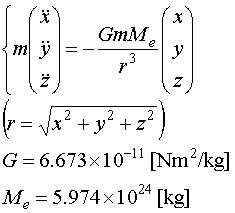
で与えられる(Meは地球の質量)
この方程式を利用して、地上 1,000km の高さから、水平方向に初速 v0 で投げ出された物体の運動を見る
アニメーションを作成せよ。
ただし地球を半径 6,378 kmの完全な球体として考え、(角運動量の保存則により軌道面が初速方向と動径方向に平行な面内にあることから)2次元の問題として考えてよい。
ちなみに、初速 7km/s の場合で、gnuplot での軌跡を表示させる手続きの
例が
/homer/pl/tea/kht23151/Examples/gnuplot/sate.gpl
にあるので、参考にすること(この例では、60秒毎で位置を描いている)。
余力のあるものは、投げ出された物体が真円軌道を描くための速度を理論的に求め、その値でアニメーションを実行させてみよ。
TOP
 ・・・ (厳密な式)
・・・ (厳密な式)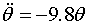 ・・・ (近似式)
・・・ (近似式)