運動方程式は x,y,vx,vyを用いて、1階の微分方程式に書き直しておく。
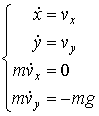
具体的に解くために、g=9.8, m=1 とした方程式を解くことにする。
初期条件としては、物体は初期時刻 t=0 で原点から速度 10 で x 軸から角度 Θ°(=th)の方向に投げ出されたとする。
すなわち x(0)=0, y(0)=0, vx(0)=10 cos(Θ), vy(0)=10sin(Θ) とおく。
オイラー法によって運動方程式を解き、そのグラフを描きます。
gnuplotを用いるので、過去の演習を参考にすること
gnuplot 入門
gnuplot と LaTeX
以下のソースコードは、2次元で y 軸方向に重力のみが働く物体の運動方程式をオイラー法によって解くものである。
運動方程式は x,y,vx,vyを用いて、1階の微分方程式に書き直しておく。
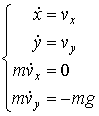
具体的に解くために、g=9.8, m=1 とした方程式を解くことにする。
初期条件としては、物体は初期時刻 t=0 で原点から速度 10 で x 軸から角度 Θ°(=th)の方向に投げ出されたとする。
すなわち x(0)=0, y(0)=0, vx(0)=10 cos(Θ), vy(0)=10sin(Θ) とおく。
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define PI 3.141592
int main(int argc,char *argv[]){
/* argc にはコマンドライン引数の数,argv には引数文字列のポインタ配列が代入される */
double t,dt;
double t1; /* t1 は終了の時刻を代入する */
double x,y,xa,ya;
double v,u,va,ua; /* u, v はそれぞれ x, y の速度を表す変数 */
double th;
th=atof(argv[1]); /* 1番目の引数文字列(角度)を数値に変換し th に代入 */
x=0.0; /* 初期位置と初期速度の設定 */
y=0.0;
v=10.0*cos(PI/180*th);
u=10.0*sin(PI/180*th);
t1=atof(argv[2]); /* 2番目の引数文字列(終了時刻)を数値に変換し t1 に代入 */
dt=atof(argv[3]); /* 3番目の引数文字列(時刻の刻み)を数値に変換し dt に代入 */
for(t=0.0; t<t1; t+=dt){
printf("%f %f\n",x,y);
xa=x+v*dt;
ya=y+u*dt;
va=v;
ua=u-9.8*dt;
x=xa;
y=ya;
v=va;
u=ua;
}
return 0;
}
このプログラムは、3つのコマンドライン引数をもちます。
第1の引数は物体の投げ出される角度Θ 、第2の引数は終了時刻、第3の引数は時間の刻み幅です。
適当な3つの引数をあたえると、物体の各時刻での座標が出力されます。
% ./a.out 45 1.5 0.05 ・・・角度45°で 1.5秒まで 0.05秒刻みで物体の座標を出力する。 (x、y座標が次々と出力される) %
課題
この出力データをファイルに出力し、それを gnuplot を用いてグラフとして出力せよ。
演習課題1のプログラムを、空気抵抗と重力を受ける物体に対する運動方程式
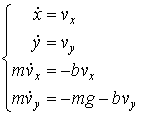
を解くプログラムに変更せよ。ただし b=1 として計算すること。
演習課題2で作成したプログラムの結果を用いて、以下の各条件でグラフを作成しそれぞれを eps ファイルとして出力せよ。
そして、以下の LaTeX ファイルに、演習課題2のソースコードと上のグラフを書き加え、コンパイルして印刷せよ。
参考資料
gnuplot と LaTeX
\documentclass[12pt]{jarticle}
\usepackage{amsmath,amssymb}
\usepackage{graphicx}
\begin{document}
\title{Euler法による放物運動の近似解について}
\author{著者名 学生番号}
\maketitle
以下の方程式は空気抵抗を考慮した重力を受ける物体が従う運動方程式である:
\begin{eqnarray}
\frac{d^2 x}{dt^2}&=&-b\frac{dx}{dt} \\
\frac{d^2 y}{dt^2}&=&-mg-b\frac{dy}{dt}
\end{eqnarray}
ここで $g$ は重力加速度、$m$ は物体の質量、$b$ は空気抵抗に関係する係数を表す。
この方程式を以下の様な条件の下で解く:
系のパラメータとして
\begin{equation}
g=9.8, m=1, b=1
\end{equation}
と設定し、初期条件としては、物体は初期時刻 $t=0$ で原点から速度$10$で
$x$軸から角度$\theta$の方向に投げ出されたとする、すなわち
\begin{equation}
x(0)=0, y(0)=0, v_x(0)=10\cos(\theta), v_y(0)=10\sin(\theta)
\end{equation}
である。
この方程式をみたす解をEuler法によって求める。
C言語によるこのプログラムのソースコードは以下の通りである:
\begin{verbatim}
この場所(\begin{verbatim}と\end{verbatim}の間)に各自が作成したソースコードを書き加える
\end{verbatim}
このプログラムは、3つのコマンドライン引数をもつ。
第1の引数は物体の投げ出される角度 $\theta$、第2の引数は終了時刻、
第3の引数は時間の刻み幅である。
このプログラムを用いて運動する物体の座標を出力し、
その座標をgnuplot を用いてグラフを出力する。
以下の3つのグラフは、コマンドライン引数を変えて
そのグラフを描いたものである。
\begin{figure}[hb]
\centering
\includegraphics[width=10cm]{ここに各自が作成したepsファイルのファイル名(1)を書く}
\caption{$\theta=45^\circ$、終了時刻$=1.5$、時間の刻み$=0.05$}
\end{figure}
\begin{figure}[hb]
\centering
\includegraphics[width=10cm]{epsファイルのファイル名(2)}
\caption{$\theta=45^\circ$、終了時刻$=1.5$、時間の刻み$=0.01$}
\end{figure}
\begin{figure}[hb]
\centering
\includegraphics[width=10cm]{epsファイルのファイル名(3)}
\caption{$\theta=40^\circ$、終了時刻$=1.5$、時間の刻み$=0.05$}
\end{figure}
\end{document}
印刷したものを提出すること。提出の締め切りは次回の演習の時間までとする。
完成見本を教卓に置くので参考にすること