中立的な価値判断に基づいて意思決定の基準を導くことができる。
第5講 微分1―微分の概念
講義の目的
1)微分を理解することの意義。
2)微分に関する基礎概念を理解する。
3)基礎的な微分の公式を理解する。
1.微分はなぜ大切か
1)政策提言における判断(意思決定)の重要性
たくさんの政策提言のなかでどの政策が有効かの意思決定を行う
例:「公共事業」(森首相)か「新分野に重点投資」(鳩山氏)か
何らかの価値判断において意思決定を行う。
意思決定の基準例
大小比較(費用便益分析)
民間企業の意思決定=利潤を最大化する(コストを最小化する)
微分は、最大値(あるいは最小値)問題を解くことにより最適解を提供する。
中立的な価値判断に基づいて意思決定の基準を導くことができる。
2.微分の定義
1)接線の傾きを求めることを微分するという
・傾き
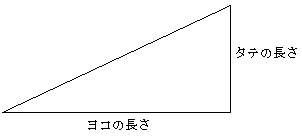
タテの長さ
直角三角形の場合、傾きは、 ━━━━━━━ で求めることができる。
ヨコの長さ
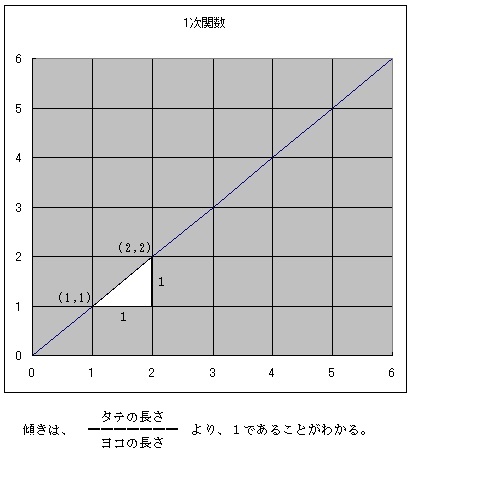
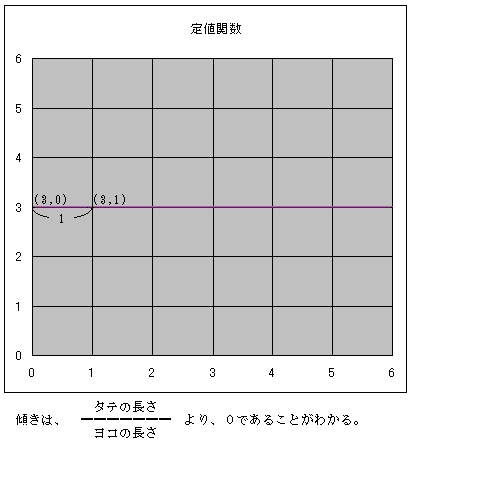
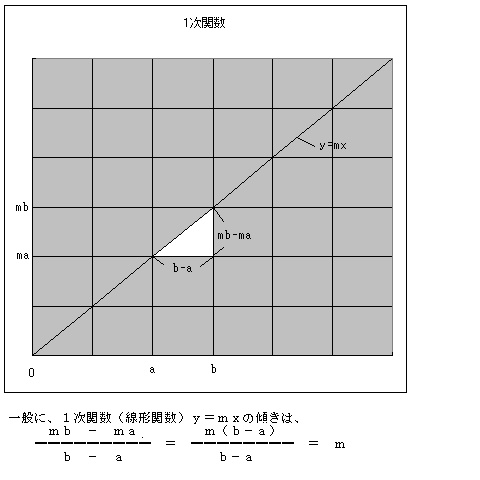

・接点と接線
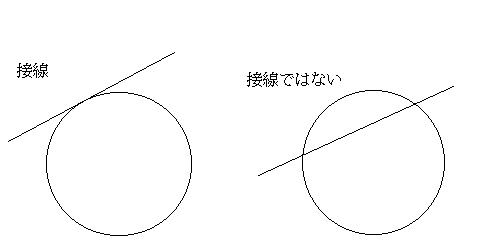
・ところで、『微分』とは?
自動車の走行距離と時間の関係をグラフを書く。(距離を縦軸に、時間を横軸にとる)
距離/時間で「平均速度」を求めることができる。
もっと細かい話は・・・瞬間速度
1分=100M 1秒=1M
もっと細かく・・・接線 ある接点における傾きがわかれば瞬間速度がわかる。
微分=接線の傾きを調べること この傾き具合がこの時点での瞬間速度
・2次関数y=x2のグラフを正確に方眼紙に書き、実際に接線を引いてみる・・・y'=2xが導かれる
微分すると傾きの式が得られる。 微分=ある関数の「導関数」を求めること。
2)lim による接線の傾きの求め方 
例:y= x2 上のある点、x = a における接線の傾きをlimで示す。
点Aと点Bの間での傾きは、
b2−a2 (b+a)(b−a)
━━━━━━ = ━━━━━━━━━━━ = b+a
b−a b−a
ここで、bをaに限りなく(極限まで)近づけると、
b2−a2 (b+a)(b−a)
lim ━━━━━━ = ━━━━━━━━━━━━ = b+a = 2a
b→a b−a b−a
点Bを限りなく点Aに近づけたときの傾きは、点Aにおける接線の傾きである。
つまり、点Aで微分したことになる。
つまり、lim は微分の定義である。
例:ある関数 y=f(x)上の任意の点x = pにおける接線の傾きをlimで示す。
f(p+h)−f(p)
lim ━━━━━━━━━
h→0 h
3.微分係数と導関数
ある点における接線の傾きを微分係数という。
ある点A(a,f(a))で接線の傾きが2ならば、Y=f(X)で、X=aのときの微分係数は「2」である。
任意の点における接線の傾きを一般的に式で示したものを導関数という。
したがって、微分とは、ある関数の導関数を求めることを意味する。
接線の傾きの式=導関数
導関数の表し方
y'、dy/dx、f'(x) で表されることがある。
4."lim"による接線の傾きの求め方
1)1次関数 y=f(x)=a+bx
f(x+h)−f(x) {a+b(x+h)}−(a+bx) bh
lim ━━━━━━━━━ = lim ━━━━━━━━━━━━━━━━━━ = lim
━━━━ = b
h→0 h h→0 h h→0 h
2)1次関数 y=f(x)=ax2
f(x+h)−f(x) a(x+h)2−ax2 a(x2+2xh+h2)−ax2
lim ━━━━━━━━━ = lim ━━━━━━━━━━━ = lim
━━━━━━━━━━━━━━━━━
h→0 h h→0 h h→0 h
2axh+ah2
= lim ━━━━━━━━━ = lim(2ax+ah) = 2ax
h→0 h h→0
5.微分の公式(導関数を求める公式)
定値関数の微分法 : y = k dy/dx = 0
線形関数(1次関数)の微分法 : y = a+bx dy/dx = b
べき関数の微分法 : y = axp dy/dx = paxp−1
和と差の微分法 : y = u(x)+v(x) dy/dx
= du/dx+dv/dx
y = u(x)−v(x) dy/dx
= du/dx−dv/dx
積の微分法 : y = u(x)v(x) dy/dx = u(dv/dx)+v(du/dx)
商の微分法 : y = u(x)/v(x) dy/dx = {(du/dx)v−u(dv/dx)}/v2
合成関数の微分法・・・y=f(u)、u=g(x)というような合成関数の導関数(dy/dx)は、最初の関数のuについての導関数と、
2番目の関数のxについての導関数の積に等しい。
: dy/dx = (dy/du)(du/dx)
演習問題
・次の関数の導関数を求めよ。
1)y = 5
2)y = −10
3)y = 2+3x
4)y = 12x
5)y = 4x3
6)y = 5x2
7)y = 12x5+4x4
8)y = 9x2+2x−3
9)y = 3x4(2x−5)
10)y = (2x4+5)(3x5−8)
11)y = (10x8−6x7)/2x
12)y = (3x8−4x7)/4x3
13)y = u4,u = 2x2+3のとき、dy/dxを求めよ。
14)y = u6,y = 3x4+5のとき、dy/dxを求めよ。