注:Machintoshではうまく表示されない場合があります。
第6講 微分2−微分と最大値最小値問題
講義の目的
1)極大・極小の概念及び極値(極大値、極小値)や最大値・最小値の求め方を理解する。
2)第2階導関数の概念を理解する。
1.関数の増減表
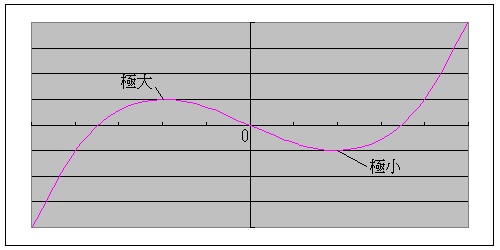
極大・極小とは・・・
ある一定の領域の中でもっとも大きい、または小さい値。
一つとは限らない。

「y=f(x)について、x=aのとき、f(x)は極大をとる」という表現をする。
f(a)という具体的な値は、「極大値」という。
「極値」という言葉は、「極大値」と「極小値」の両方を指す。
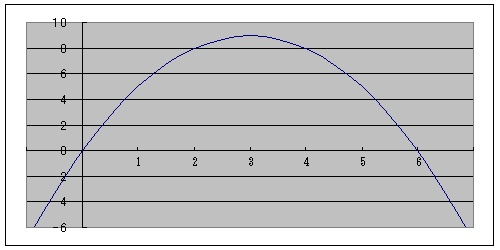
例1:2次関数 y = −x2 + 6x の増減
<平方完成>
y = −x2 + 6x =(x−3)2+9 より、グラフを描く。
x = 3のとき極大値9をとることがわかる。
<微分>
導関数 y´= −2x − 6 = −2(x − 3) から以下のことがわかる。
y´> 0 となるxの範囲は、x < 3
このとき、接線の傾き y´はプラスであるからグラフは右上がり。
y の値は、x の増加とともに増加する。
y´< 0 となるxの範囲は、x > 3
このとき、接線の傾き y´はマイナスであるからグラフは右下がり。
y の値は、x の増加とともに減少する。
y´= 0 となるxの範囲は、x = 3
このとき、接線の傾き y´はゼロ(0)であり2次関数の頂点となる。
y の値は、x の増加とともに増加する。
以上のことは「増減表」で簡潔に示すことができる。
増減表
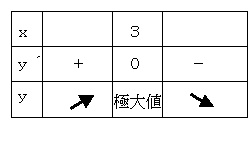
x < 3のとき y´> 0(接線の傾きが正)
x = 3のとき y´= 0(接線の傾きが0)
x > 3のとき y´< 0(接線の傾きが負)
y´= 0で極大値 y = 9 をとる。
(ここでは最大値であり、最適解を得ることができる)
ただし、y´= 0 は極値を求めることはできても、それが、極大値か極小値か決めることができない。
(たとえば、y = x2 では y´= 0 のとき、極小値を取る。)
必ずしも極大値を得られない・・・y"(第2階導関数)が正か負で極大・極小の区別ができる。
例2:3次関数y = x3 − 3x の増減
導関数 y´ = 3x2 − 3 = 3(x + 1)(x − 1)
増減表
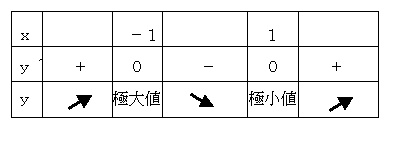
極大 x = −1 のとき、極大値 y = 2
極小 x = 1 のとき、極小値 y = −2
2.第2階導関数の概念
1)距離、速度、加速度 の関係
y = f(x)で、yを距離、xを時間とした場合、
y´ = f´(x) 距離を時間で微分・・・速度
y" = f" (x) 速度を時間で微分・・・加速度
y" > 0・・・時間とともに加速 速度は速くなる
y" < 0・・・ 減速 遅くなる
2)第2階導関数は「接線の傾きの変化」を示す。
y´は接線の傾き、y" は接線の傾きの変化 を示す
y" >0・・・接線の傾きは逓増する
y" <0・・・接線の傾きは逓減する
増減表を書かなくても極大・極小がわかる。
3)y = f(x) において、f´(a) = 0 であるとき、
f" (x) > 0 ならば、f(x) は x
= a で極小
f" (x) < 0 ならば、f(x) は x
= a で極大
一般的に、y´ = f´(x) = 0 を満たすxに対応するyが極値をとることはわかる。
しかしそれが、極大値か極小値かはわからない。極大値か極小値かの情報を得るためには、第2階導関数を求める必要がある。
例2の場合、y" = 6x したがって
x = 1のとき、y" >0 であるから、y = −2は極小値
x = −1のとき、y" <0 であるから、y = 2は極大値 となる。
3.最大最小値問題
例:次の関数の最大値と最小値を指定された定義域(xの範囲)内で求めよ。
y = 2x3 − 9x2 (−1 ≦ x ≦ 5)
導関数 y´ = 6x2 − 18x = 6x(x − 3)
増減表
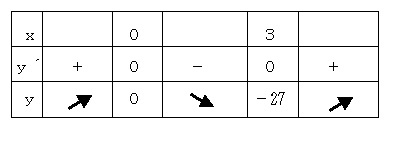
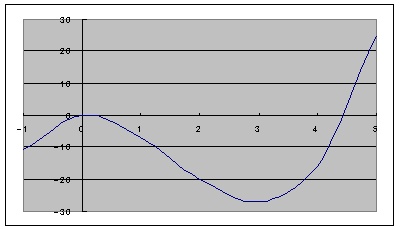
したがって、x = 5 のとき、最大値 y = 25
x = 3 のとき、最小値 y = −27
x = 0、y = 0 ・・・極大であるが最大ではない。
x = 3、y = −27 ・・・極小かつ最小である。
演習問題
(1)y = 12x − x3 の増減表をつくり、極値を調べよ。また、増減表を使用せずに第2階導関数を用いて極値を求めよ。
(2)y = x3 − 6x2 + 9x の増減表をつくり、極値を調べよ。また、増減表を使用せずに第2階導関数を用いて極値を求めよ。
(3)たて3cm、横8cmの長方形のブリキ板の四隅から、一辺xcmの正方形を切り取り、ふたのない容器を作る。
容器の容積ycm3を最大にするには、切り取る正方形の一辺の長さを何cmにすればよいか。