第7講 微分3-微分と社会科学への応用
1.講義の目的
微分が社会科学の分野(特に経済学の分野)でどのように利用されているかをいくつかの事例を上げて説明する。
具体的には、「限界概念」・企業の利潤最大化条件・「弾力性」について理解を深める。
2.限界概念-費用関数を事例に
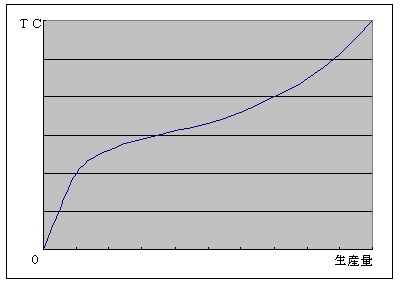
費用関数 TC = C(q) 総費用を示す。一般に、総費用=固定費用+変動費用
ここでは、総費用は変動費用の関数であるとする。

平均費用 AC = C(q)/q 生産物1単位あたりの費用 (総費用÷生産量)
限界費用 MC = C´(q) 生産量が一単位増加したときの費用の増加分。
ある点における微分係数 dTC/dq(TC´、または⊿TC/⊿q)。
限界費用逓増の法則 C"(q) > 0
従来の製造業では成り立つが、ソフト開発では、コピーに費用がほとんどかからないので、
この法則が成り立たなくなる可能性が指摘されている。
3.利潤最大化の条件
1)生産が非連続の場合
例:表 スーツ縫製企業の費用と利潤
スーツの価格を4万円とする。
|
X |
TR |
TC |
π=TR-TC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
MR=P |
MC |
MP=MR-MC |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
限界収入=一着販売を増やしたときにどれだけ収入が増えるか
限界利潤(=価格-限界費用)が正である限り、生産量を増やすほうが利潤は増大する。
結局この例では、利潤最大となるのは、生産量が8の時である。
2)生産量が連続の場合
π = pq - C(q) p:価格 q:生産量 π:利潤
dπ/dq = p - C´(q)
p = C´(q) のとき、すなわち、価格=限界費用 のとき、dπ/dq = 0(極値をとる)
最大値条件を満たすためには、第2階導関数が負になる必要がある。
第2階導関数: -C"(q) < 0
限界費用逓増の法則を仮定すると上記の条件は満たされる。よって利潤最大化の条件は、
限界費用逓増の法則を前提とした場合、価格=限界費用 である。
3.弾力性の概念-需要の価格弾力性を事例にして
需要の価格弾力性の定義
⊿x/x
η = ━━━━━━
⊿p/p
価格の変化に対応して、需要量がどの程度変化を表す指標。
必需財:価格が上昇しても、それほど需要量を減らすわけにはいかない。
・・・需要の価格弾力性が小さい(非弾力的)。
奢侈品:価格が低下すれば、それだけ需要が増える。
・・・需要の価格弾力性が大きい。(弾力的)
演習問題
(1)在庫問題
ある商事会社で扱うある製品の売上量が1200単位であるとする。
この品物を年間何回かに分けて発注することにする。
1回の発注量はいつも同じにするとして、最も経済的な発注量を定めよ。
製品は、単価5,000円、1単位を1年間在庫させるのに要する費用は単価の10%、
1回の発注に必要な諸経費は7,000円であるとする。
(2)ある企業におけるある生産財について、その費用関数が、
c = q2 + 100 と与えられている。このとき、以下の問いに答えよ。
1)限界費用関数と、平均費用関数を求めよ。
2)この財の市場価格が50ならば、生産量はいくらのとき、利潤は最大となるか。