Exact Solution for Advection Equation - 3

　初期条件である(8)式をグラフ化したものがFig.6における黒線です。ここで，初期状態の波がx軸の正の方向（正確にはkx軸方向･･･あまり気にしないでください）へ移流速度uでt時間流された場を考えましょう。すると，Fig.6における青線が示すように，t時間後の波は初期状態の波がx軸の正の方向へut平行移動したものになります。

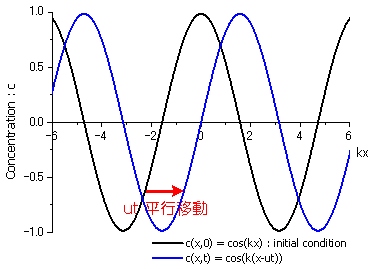Fig.6　t秒後の波形（青色）

以上より，t時間後の波は次式によって表すことが出来ます。

(10)

(10)式は，「x-ut」がx軸の正の方向へut平行移動することを表しています。

　初期条件である(8)式とt時間後の状態（解析解）である(10)式を比較してみましょう。(8)式における「x」が，(10)式において「x-ut」に変化しただけと気が付くでしょう。これは，(7)式の示すものと全く同じですね（この場合の関数fとは「cos」のことです･･･初期条件を設定することで関数fが決まります）。