![]()
Numerical Solution By Explicit-FTCS - 7
![]()
■ プログラムの実行結果 ■
exftcs.fを実行すると次の出力ファイルが出てくるはずです。
| 出力ファイル | 説明 |
| input__.dat(例) | 解析に使用したパラメータを記録しています。 |
| output__.dat(例) | 解析結果(解析終了時刻における汚染濃度の値(近似解))を記録しています。位置x、汚染濃度cという順番に並んでいます。 |
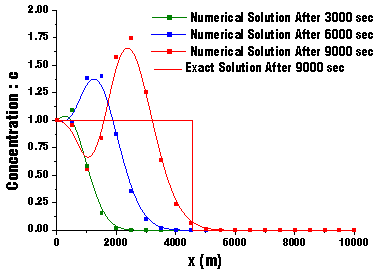
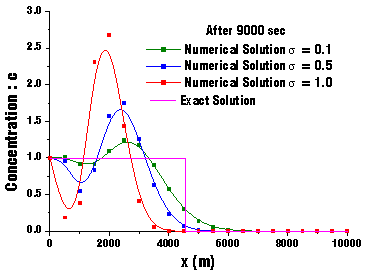
output__.datをグラフ化させたものを,Fig.17,Fig.18に示します。Fig.17の入力条件は,TT=3000,6000,9000,XX=10000,⊿t=500,⊿x=500,u=0.5,σ=0.5です。また,Fig.18の入力条件は,TT=9000,XX=10000,⊿t=100,500,1000,⊿x=500,u=0.5,σ=0.1,0.5,1.0です。なお,初期条件はc(x,0)=0,境界条件はc(0,t)=1です。
 |
 |
|
| Fig.17 解析解と近似解(陽解式FTCS)の比較 | Fig.18 無次元パラメータσの影響 |
Fig.17を見てください。Fig.17は,移流方程式の解析解と陽解式FTCS近似解を比較したものです。x=0の地点より汚染物質が注入されており,それが時間が経つにつれてxの正の方向へ流されているのがわかります。ここで,近似解に着目してください。陽解式FTCS差分法より得られた近似解は何やら波の形をしていますね。はたしてこれは正しいのでしょうか。答えはノーです。なぜなら,移流という現象は,汚染物質が流れよって流されるだけの現象ですので,汚染濃度が増幅したり減衰したりすることはありません(この場合,汚染濃度は0か1しか取りえません)。
次に,Fig.18を見てください。Fig.18は無次元パラメータσの値が近似解に及ぼす影響を調べたものです。σが大きくなるにつれて,近似解の振幅が大きく(不安定)なりそうですね。一方,σが小さくなるについれて,近似解の振幅は小さくなりますが,横方向(x軸方向)のズレが大きくなりそうですね。なお,無次元パラメータを変化させるということは,刻み幅⊿x,⊿tを変化させるということです。
Fig.17及びFig.18を見て以下のことが推測できます。
1. 陽解式FTCS差分法により得られた近似解は必ず不安定(発散)になる(振幅が増大しているからです)。
2. σを小さくするほど,発散量は小さくなる。しかし,横方向のズレが大きくなってしまう。
3. 陽解式FTCS差分法では,安定した近似解を得ることはできないが,不安定ながらも精度良い近似解を得るためには,σを小さく且つ解析時間を小さくする必要がある(コレでも,結構無理があります)。
■ ちょっと一言 ■
結局のところ,移流方程式の近似解を求めるために,陽解式FTCS差分法を適用しても全然ダメということがわかりましたね。後ほど説明しますが,陽解式CTCS差分法(通称LeapFrog法)を適用するとかなりマシになります。しかし,LeapFrog法を使って移流方程式の近似解を求めて,必ずその解が安定し精度良いのかというとそうでもありません。
「じゃあ,どれもダメじゃん」ということになりますが,その通りです。そもそも,差分法というものは移流方程式の近似解法には向いていません。移流方程式を安定し精度良く近似計算を行うには,別の近似解法(例えば,特性曲線法など)を使います。どうしても,差分法を適用する場合には,上で述べたLeapFrog法や風上法などが用いられれます。興味ある人は勉強してみてください。
| Back | Next | |||
| Advection Equation | Exact Solution |
Numerical Solution By Ex-FTCS Method |
Numerical Solution By Ex-CTCS Method |