Numerical Solution By Explicit-FTCS - 8

■　増幅率の計算の前に･･･　■

　陽解式FTCS差分法の安定性と精度について考察してみましょう。一階線形常微分方程式のときと同様に，増幅率の観点から考えてみます。しかし，偏微分方程式の数値解増幅率は，常微分方程式のように簡単に求めることはできません。求めるためには，フーリエ展開や複素数計算を利用する必要があります（別の方法もあります･･･）。

　さて，移流方程式の増幅率を次のように定義しましょう。

(23)

一方，移流方程式の陽解式FTCS差分方程式を以下に再載します。

(15，再載)

陽解式FTCS差分法の数値解増幅率ρを求めるためには，(15)式を(23)式の形へと変形する必要があります。どうです，変形できますか？見るからにできそうにありませんね（cⁿ_j+1とcⁿ_j-1が邪魔ですね･･･）。このままでは(15)式を(23)式に変形することはできません。しかし，(15)式に対して，とある手続きを行えば，(23)式に変形することができます。その手続きとは「フーリエ展開」です。

■　陽解式FTCS差分法の数値解増幅率ρ（具体例）　■

　フーリエ展開うんぬんの話は後にして，とりあえず，ある状態を仮定して陽解式FTCS差分法の数値解増幅率を計算してみましょう。増幅率を求めるには，(23)式が示すように，ある任意の時刻tにおける汚染濃度の値が既知でなくてはなりません。そこで，任意の時刻tにおける汚染濃度分布を次のように仮定してみましょう。

(24a)

または，

(24b)

ちょっと見慣れないかもしれませんね。(24)式は，任意の時刻t（固定）における汚染濃度分布を仮定したものです。したがって，独立変数はxのみとなっております（t=tのときなので･･･）。(24)式の仮定により，(15)式を用いれば，t=t+�冲における汚染濃度分布が次のように計算できますね。

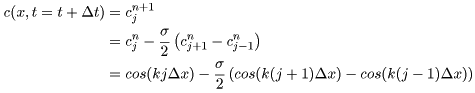(25)

さて，c(x,t)とc(x,t+�冲)が(24)式および(25)式で求まりました。したがって，(23)式から増幅率を計算してみましょう･･･，と思ってもキレイに計算できませんね。増幅率を求めるには，(25)式を(24)式で割ることになるので，cos同士の割り算が出てきてしまいます。皆さんもご存知のように，三角関数の掛け算や割り算は非常に面倒です。

　三角関数の演算を簡単にする手法として，複素数を利用する方法があります。では複素数を使って，増幅率を計算してみましょう。まず，(24)式を複素数で表わすと次のようになります（証明は，各自で調べてください）。

(26)

isin(kj�凅)の項は虚部と呼ばれ，数ではありません。とりあえず(24)式と(26)式は同一のものと考えてください。同様に，cⁿ_j+1は，e^{ik(j+1)�凅}と表わされ，cⁿ_j-1は，e^{ik(j-1)�凅}と表わされます。したがって，cⁿ⁺¹_jは，(15)式を用いて次のように計算できます。

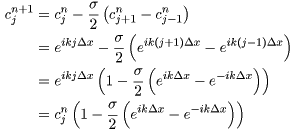(27)

　ここで，(27)式中のe^ik�凅-e^-ik�凅について考えてみましょう。e^ik�凅については，次式で表わされますね。

(28)

一方，e^-ik�凅については，次式で表わされます。

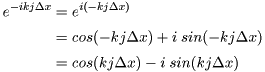(29)

したがって，(28)式から(29)式を引けば，e^ik�凅-e^-ik�凅が計算できます。

(30)

　(27)式に，(30)式を代入すれば，次式のようになりますね。

(31)

したがって，数値解増幅率ρは，次式のように求まります。

(32)

　さてさて，なんだかんだ言って，数値解増幅率ρが計算できました。なぜ計算できたかというと，t=tⁿにおける汚染濃度分布が(24)式のような三角関数で仮定されていたからです。 では，もしt=tⁿにおける汚染濃度分布が三角関数でなかったら(32)式は間違いである･･･ということになりますね。そのことについては次頁に述べます。