Numerical Solution By Explicit-FTCS - 9

■　陽解式FTCS差分法の数値解増幅率ρ　■

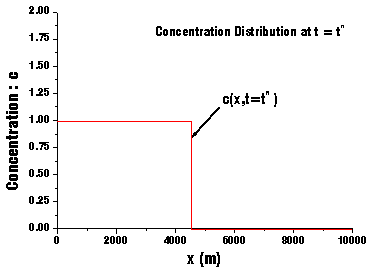
　もしt=tⁿにおける汚染濃度分布が三角関数でなかったら，数値解増幅率ρはどうなるのでしょう。例えば，t=tⁿにおける汚染濃度分布がFig.19のような形で与えられたらどうでしょう。

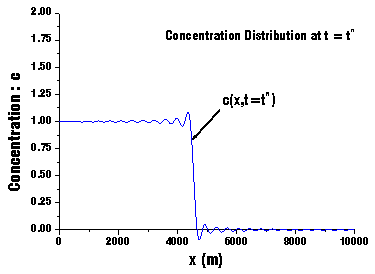
Fig.19　時刻tにおける汚染濃度分布		Fig.20　時刻tにおける汚染濃度分布をフーリエ近似

どこを，どう見ても三角関数に見えませんね。したがって，このときの移流方程式の数値解増幅率ρは(32)式ではありません。 しかしながら，このときの数値解増幅率ρは(32)式に非常に似たような式で表わされます。

　さて，t=tⁿにおける汚染濃度分布がFig.19のようなある任意関数c(x,t=tⁿ)で表わされているとします。このc(x,t=tⁿ)はどのような関数になっているかは私たちにはわかりません。 どのような関数かは分かりませんが，この関数は，三角関数の和で近似できることはフーリエによって証明されております（この場合に限らず，どのような関数（周期関数）でも三角関数の和で表現できます）。 その近似手法がフーリエ展開であり，近似された関数をフーリエ級数と呼びます。
　さて，Fig.19に示すような関数c(x,t=tⁿ)をフーリエ級数で表わしてみましょう。その変換式は次式を用います（フーリエ余弦展開といいます）。 なお，c(x,t=tⁿ)を以下c(x)^(t=tn)と表示します。時刻tにおける関数c(x)ということです。なお， フーリエ展開については，個人で勉強してください。

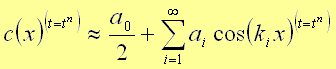(33a)

ここに，

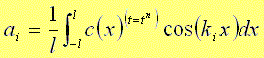	(33b)
	(33c)

なお，(33)式中のlとは半周期を表わしています（2lで一周期です）。(33a)式で表わされるフーリエ級数をグラフ化したものがFig.20です。Fig.19とFig.20を見てみますと，結構イイ感じに近似されていますね。

　では，任意の時刻tにおける汚染濃度分布がある関数c(x,t=t)で表わされたときの，数値解増幅率ρについて考えてみましょう。c(x,t=t)に対して，(33a)式に示すフーリエ展開を行えば， (15)式中のcⁿ_j，cⁿ_j+1，cⁿ_j-1は次のようになります（複素数表示です）。

	(34,a)
	(34,b)
	(34,c)

したがって，(15)式より，cⁿ⁺¹_jは次のように求まります。

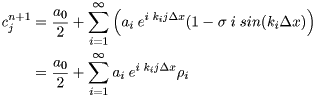(35)

ここで，パラメータρ_iを次のように定義しています。

(36)

(34,a)式と(35)式を比較してみましょう。(35)式は，(34,a)式の一番最後にパラメータρ_iが引っ付いているだけですね。これがどういう意味かわかりますか？ (34,a)式におけるi番目のcos波であるa_ie^ik_ij�凅が，1時間ステップ進むとρ_i倍されるということです。 したがって，ρ_iの絶対値が1を越えるとi番目のcos波は発散するので，cⁿ⁺¹_jは発散してしまいます。

　頭がグチャグチャになってしまいそうですね。以下に，この頁の内容をまとめます。
　移流方程式の数値解増幅率を計算する場合，陽解式FTCS差分方程式である(15)式のみから増幅率は計算することができない。 そこである任意の時刻t（n時間ステップ目）における汚染濃度分布c(x,t=tⁿ)をフーリエ展開することを考える。汚染濃度分布c(x,t=tⁿ)が，厳密にどのような関数で表わされるはわからないが， c(x,t=tⁿ)をフーリエ近似を行えば，それは三角関数の和で必ず表現されるハズなので，その三角関数を利用して増幅率を考える･･･，ということです。
　その結果，移流方程式の陽解式FTCS差分法の近似解が発散しない条件「(36)式に示すρ_iの絶対値が1より小さいこと」が得られます。したがって，ρ_i の絶対値が1を越えないようにσおよび�凅を設定しなくてはなりません（k_iは定数ですので，関係ないですよ）。
結局，(36)式の絶対値が1より小さいことと，(32)式の絶対値が1より小さいこととは全く同じことです。
　増幅率を計算する場合，ある任意の時刻tにおける汚染濃度分布をc(x,t=tⁿ)とおき，それをフーリエ展開していく･･･という作業を行わなくても，ある任意の時刻tにおける汚染濃度分布を (24)式のように1つの三角関数で仮定して増幅率を計算していく事ができるということです。