![]()
Numerical Solution By Explicit Method - 2
![]()
仭丂堦奒慄宍忢旝暘曽掱幃偺嵎暘夝朄丂仭
丂偝偰丆(4)幃傪嵎暘朄傪梡偄偰嬤帡揑偵夝偄偰傒傑偟傚偆丅慜崁偺偲偍傝偵丆愢柧傪偟偰偄偒傑偡丅偄偒側傝偺偙偲偱媈栤偵巚偆偙偲偑懡乆偁傞偐偲巚偄傑偡偑丆偲傝偁偊偢丆埲壓偺偲偍傝儅僱偟偰偔偩偝偄丅
仭丂撈棫曄悢傪棧嶶壔偡傞丂仭
丂(4)幃偺撈棫曄悢偼丆帪娫t偱偡偹丅偪側傒偵丆墭愼擹搙c偼廬懏曄悢偱偡乮t偑寛傑傞偙偲偵傛偭偰丆c偑寛傑傞乯丅偝偰丆t偼楢懕検側偺偱丆偙傟傪棧嶶検偵曄姺偟傑偡丅Fig.3偺傛偆偵丆t幉傪嚈t偺娫妘偱丆NT摍暘偟傑偡丅
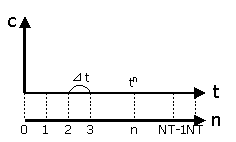 |
| Fig.3丂t幉傪嚈t娫妘偱NT摍暘偡傞 |
偙偙偵丆
| 丂丂丂丂丂(14) |
偲偄偆娭學偑惉傝棫偪傑偡偹丅
仭丂旝暘曽掱幃偐傜嵎暘曽掱幃傊曄姺乮梲夝朄乯丂仭
丂(4)幃傕楢懕検側偺偱丆偙偺曽掱幃傕棧嶶壔偡傞昁梫偑偁傝傑偡丅偙偙偱偼丆嵎暘朄傪梡偄偰棧嶶壔偟傑偡丅
| 丂丂丂丂丂(4丆嵞嵹) |
dc/dt偵偮偄偰峫偊偰傒傑偟傚偆丅dc/dt傪棧嶶検偵曄壔偝偣傞昁梫偑偁傞偺偱偡偑丆偙傟偼師偺傛偆偵棧嶶壔偝偣傑偡乮崅峑帪戙偵廗偭偰偄傞偼偢偱偡乯丅
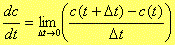 |
丂丂丂丂丂(15) |
偟偐偟丄儮t偼偄偔傜彫偝偔偰傕桳尷偺悢抣側偺偱乬亖乭偺戙傢傝偵乬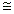 乭偵側傝傑偡丅
乭偵側傝傑偡丅
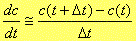 |
丂丂丂丂丂(15a) |
偙偙偱丆t傪tn,t+儮t傪tn+1丆c(t)傪cn,c+儮t傪cn+1偲抲偒傑偡丅偡傞偲丄乮15a乯幃偼師偺傛偆偵側傝傑偡丅
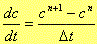 |
丂丂丂丂丂(15b) |
偝偰丆師偵峫偊側偔偰偼側傜側偄偺偼丆(15)幃偺dc/dt傪丆嬫娫[t,t+嚈t]偺娫偺偳偺揰傪昡壙偡傞偺偐偲偄偆偙偲偱偡丅 偙偙偱偼丆dc/dt傪t=tn偺揰偵偰昡壙偟傑偡丅 懄偪丆乮4G乯幃傛傝,
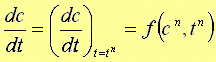 |
丂丂丂丂丂(16G) |
偟偨偑偭偰丆(15)丆(16)幃傛傝丆(4G)幃偵偍偗傞嵎暘曽掱幃偑師偺傛偆偵摫偐傟傑偡丅
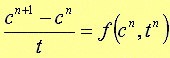 |
丂丂丂丂丂(17G) |
偝傜偵丄(17G)幃傪曄宍偡傟偽丆師幃偺傛偆偵側傝傑偡丅
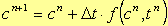 |
丂丂丂丂丂(18G) |
偄傑丄嬶懱椺偲偟偰4幃偺塃曈傪f偺偲偙傠偵戙擖偡傞偲師幃偺傛偆偵側傝傑偡丅
| 丂丂丂丂丂(18) |
| Back | Next | |||
| 1st-order linear O.D.E |
Exact Solution |
Numerical Solution By Explicit Method |
Numerical Solution By Implicit Method |