Numerical Solution By Implicit Method - 1

■　微分方程式から差分方程式へ変換（陰解法）　■

　さて，前項で説明した近似解法は，陽解式差分法です。結論から言いますと，この陽解法は，精度や安定性において優れている解法ではありません。このため，今日では，本項で述べる陰解法がよく用いられます。ここでは，(4)式を陰解法で解く方法を学びます。

(4，再載)

陰解法でも同様に，(4)式を離散化します。dc/dtは以下のように離散化されます。

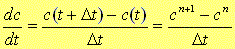(15a)式および(15b)式

さて，ここで重要なことは，(15)式のdc/dtを，区間[t,t+�冲]の間のどの点を評価するのかということでしたね。 陽解法では， dc/dtをt=tⁿの点にて評価しましたが，陰解法では，dc/dtをt=tⁿ+θ�冲にて評価します（Fig.10参照）。

Fig.10　dc/dtの評価方法（赤：陽解法，青：陰解法）

dc/dtがtⁿからtⁿ+Δtの間に線形的に変化していると仮定すると，tⁿにおけるdc/dtを次式で評価できます。

(32)

(4)，(15)，(32)式より陰解式差分方程式が次のように導かれます。

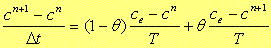(33)

次に未知変数であるcⁿ⁺¹を求めたいと思います。
今回扱っている(33)式はcⁿ⁺¹に関して線形であるので，(33)式を変形すれば，次式のようになります。

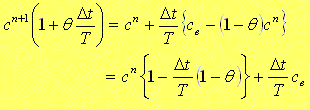(34)

さらに両辺を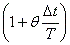で割ると、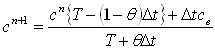のような陽式が得られます。