Numerical Solution By Explicit Method - 6

■　解析解増幅率ρ_aと精度　■

　次に，解析解の増幅率ρ_aについて考えてみましょう。増幅率は(23)式のように，で定義されているので，(4)式もで表わてみましょう。(4)式をで表わすと次式で表わされます。

(27)

続いて，(27)式の解析解は次式で表わされます。

(28)

　さて，解析解増幅率ρ_aを求めてみましょう。
　増幅率は(23)式で示すように，t=n�冲におけるとt=(n+1)�冲におけるの比で定義されています。つまり，�冲進んだとき，がどのくらい増幅されるかを示しています。このことを考慮すれば，解析解増幅率ρ_aは次式で求めることができます。

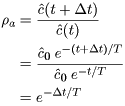(29)

解析解増幅率ρ_aと数値解増幅率ρを比較してみましょう。そのグラフをFig.9に示します。

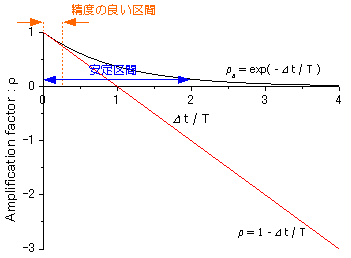Fig.9　解析解増幅率ρaと数値解増幅率ρの比較

　さて，ここで精度について考えてみましょう。精度が良いということは，解析解増幅率ρ_aと数値解増幅率ρが漸近しているということです。Fig.9を見ていただければわかるように，ρ_aとρが漸近するのは，おおむね，次の条件を満たすときです。

(30)

(30)式を満たすとき，近似解の精度は良いということになります。

■　最適な刻み幅�冲　■

　最後に，(4)式を陽解式差分法により近似解を求める際の注意事項についてまとめます。
　差分法において，刻み幅�冲を不適切に設定してしまうと，精度が悪いだけでなく不安定な解を計算してしまう恐れがあります。そのため，適切な�冲を設定する必要があります。

　その�冲は，次の条件から決定していきます。
1.　安定した解を得ること（絶対必要条件）
2.　精度の良い解を得ること

　1.の条件については(26)式ですね。2.の条件については(30)式ですね。したがって，(26)式および(30)式を同時に満たすときが最適な�冲となります。即ち，

(31)

の条件を満たす�冲が，最適な値となります（まぁ，Fig.9を見れば一目瞭然ですね）。