Numerical Solution By Explicit Method - 5

■　増幅率　■

　近似解を得るためには，刻み幅�冲を設定する必要があります。しかしながら，この刻み幅�冲が解析に不適切な（�冲が大きすぎる）値だと，解が不安定になってしまいます（Fig.6のdt=2.5の状態）。
したがって，近似解を得る際には，�冲の最低条件として，解が不安定にならないような刻み幅�冲を設定する必要があります。さらに精度を上げるためにΔtに関する条件がでますが,それは次のページで説明します。

　不安定にならないような刻み幅�冲はどのようにしたら求められるのでしょうか？(4)式のような線形上微分方程式においては，増幅率という概念を用いることによって，求めることできます。では，増幅率を使って，不安定にならないような刻み幅�冲を求めてみましょう。

■　数値解増幅率ρと安定条件　■

　陽解式差分方程式(18)式を次のように変形します。

(21)

ここで，，と定義し，(21)式に代入すると次式のようになります。なお，Fig.7は増幅率ρのグラフを示します。

(22)	Fig.7　�冲/Tに対する増幅率ρの変化

　さて，増幅率ρを別の角度から見てみましょう。(22)式より，増幅率ρは次式でも表わすことができますね。

(23)

高校で習った数列の知識を使えば，(23)式を，公比ρである等比数列{}とみなすことができますね。ここで，等比数列の特徴を思い出してください。その特徴を以下の表にまとめます。

{}の変化

(24) 収束（安定） のとき，振動なし のとき，振動あり 　　　　　(25) 発散（不安定）

注目していただきたいのは，(25)式です。
増幅率ρの絶対値が1より大きいのとき，数列{}は発散します。 が発散すれば，近似解cⁿ (=+c_e)も発散します。 したがって，陽解式差分方程式から得られる近似解が発散しない条件は，増幅率ρの絶対値が1以下のときです。 つまり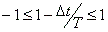，のときであり，これを解けば，

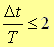(26)

という安定条件が得られます（Fig.7参考）。

　（4）式に対して，陽解式差分方程式から近似解を求めようとする際には，最低限，(26)式を満足するような刻み幅�冲を設定しなくてはなりません。Fig.7に安定する区間を加筆したものを，Fig.8に示します。

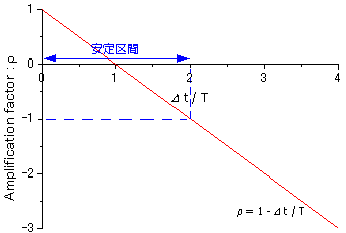Fig.8　安定区間