1st-order linear Ordinary Differential Equation - 2

■　支配方程式の導出方法　■

　Fig.1内で起きている現象を表す式を導きます。現象を表す式（基礎方程式）を導くには，
1.　質量保存則
2.　運動量保存則
3.　エネルギー保存則
が必要になります。一般に，2，3番目の保存則は現象に外力が関与する場合に用いられます。
　ここでは，ただ純粋に汚染物質の挙動を調べたいだけなので，質量保存則をたてるだけで十分です（流れによって水圧がどう変化するのか･･･といった問題に対して2，3番目の保存則が必要になります）。

■　減衰現象　■

　まずFig.1における，Degradation（減衰）について説明します。
　湖内にある汚染物資は，微生物によって分解されます。すると，当然，汚染物質の量は低下します。その低下量は，Vc/T_rの形で表わされています。 さて，湖の体積がVであるということを考慮すれば，

(6)

ということがわかります。つまり，減衰現象による汚染物質の低下量は，汚染濃度cに比例し，反応時間T_rに反比例することになります。
このことを常微分方程式で表すと

　　 　　　　

(6a)

　　 　　　　

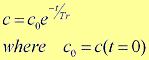(6b)

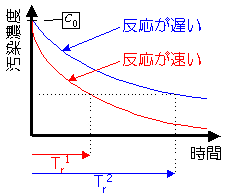Fig.2　汚染物質と微生物の分解反応の経時変化

反応時間T_rとは，所定の汚染濃度にまで低下させる時間のことをいいます。したがって，分解反応が速く進めば（汚染濃度が大きく低下したら），T_rは小さくなります。 したがって，汚染物質の低下量は，T_rに反比例しますね。また，汚染濃度が大きく低下するのは，汚染濃度が高いときです。したがって，汚染物質の低下量は，cに比例します。