![]()
1st-order linear Ordinary Differential Equation - 3
![]()
■ 質量保存側 ■
Fig.1において,汚染物質の質量保存則を考えます。質量保存側は次式で表わされます。
| (1) |
(1)の各項の内訳は次のようになります。皆さんも試してみてください。
| コントロールボリューム内での 単位時間当たりの質量変化 |
|
| 流入質量 | |
| 流出質量 |
したがって,湖内での質量保存側すなわち支配方程式は次式で表わされます。
| (2) |
ここに,c:汚染濃度[M/L3],Tr:反応時間[T]を表わします。
■ 水理学的な定常とは ■
この段階ではV=const、すなわちと仮定します。ここで(2)式が、次の(2a)式のように変形できます。
(つまり、Vが定数となって外に出せる)
 |
(2a) |
■ 支配方程式 ■
Fig.1内で起きている現象は,(2a)式で表わされるということがわかりました。
さて,(2a)式をさらに簡略化しましょう。
(2a)式において,変数はcのみとして,他のパラメータはすべて一定とします。
式(2a)をよりわかり易くするために、まずは定常状態(dc/dt = 0)について考えてみましょう。このときの濃度を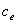 と置き、(2a)式から下記のような結果が導き出される。
と置き、(2a)式から下記のような結果が導き出される。
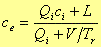 |
(3) |
(2a),(3)式より,最終的な支配方程式は次式で表わされます。
| (4) |
ここに,パラメータTを次のように定義します。
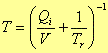 |
(5) |
≪5月14日に追加しました≫
ここで、一般式について考えたいと思います。一般的な一次常微分方程式は下記の形になります:
| dc/dt = f(c,t) | (4G) |
(4)式と比べると、右辺に従属変数であるcおよび独立変数のtの任意関数がある。
(※:式番号の添え字“G”は、“General case”=“一般式”を表しています 。)
| Back | Next | |||
| 1st-order linear O.D.E |
Exact Solution |
Numerical Solution By Explicit Method |
Numerical Solution By Implicit Method |