Numerical Solution By Explicit-FTCS Method - 2

■　近似解を求めるために　■

　差分法を用いて微分方程式の近似解を求めるためには，
1.　独立変数を離散化する
2.　微分方程式から差分方程式へ変換
3.　プログラムの作成及び実行
をする必要がありますがありましたね（一階線形常微分方程式の頁を参照）。

　移流方程式の近似解を求める際も，上記と同様のステップを踏んでいきます。

■　独立変数を離散化する　■

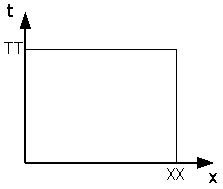
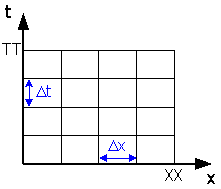
　移流方程式の独立変数は，時間tと位置xですね。さて，tおよびxは連続量なので，これを離散量に変換します。Fig.3のように，t軸を�冲の間隔でNT等分して，一方x軸を�凅の間隔でNX等分します。

(a)　連続空間	(b)　連続空間を離散化 Fig.7　連続量から離散量へ	(c)　離散空間

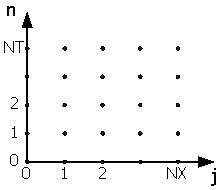
Fig.7は，移流方程式の独立変数tおよびxを離散化している過程を示しています。移流方程式をx-t座標系で表現するとFig.7(a)のようになりますね（従属変数である汚染濃度cの軸は，x-t平面に垂直な方向にあると考えてください）。この解析空間を，Fig.7(b)のように，離散化（メッシュ）します。すると，Fig.7(c)のような離散空間が生まれます。この図を格子図と呼びます。
　Fig.7(c)において，各々の点を節点といい，ある節点に対応するj，nを節点番号といいます。また，連続量と離散量の間には次のような関係があります。

(11)

ここに，n：時間軸に対応する節点番号，j：空間軸に対応する節点番号，tⁿ：節点番号nに対応する時間[T]，x_j：節点番号jに対応する位置[L]，�冲：時間刻み幅[T]，�凅：空間刻み幅[L]を表わします。

差分法で近似解を求める際には、Fig.7(c)のような格子図上で議論していくことになります。