Numerical Solution By Explicit-FTCS Method - 3

■　微分方程式から差分方程式へ変換　■

　先ほども申しましたが，差分法では微分方程式中の連続量を離散化させ，議論を進めていきます。したがって，与えられた条件（微分方程式，初期条件，境界条件等･･･）も全て，離散量に変化させる必要があります。微分方程式を離散化させたもの，それが差分方程式です。
　差分方程式を導く前に，(4)式における変数cの格子図上での表記方法を定義しましょう。Fig.8のように，格子図上の任意の節点におけるcの値をcⁿ_jと定義します。

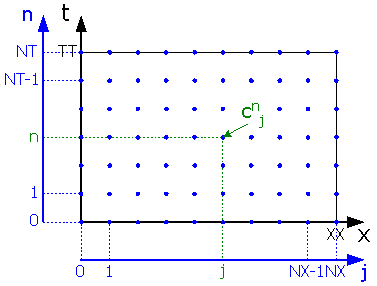Fig.8　変数cの表記方法の説明図

　さて，本題に入りましょう。(4)式を陽解式-FTCS差分法で差分方程式を導いてみましょう。FTCSとは，「時間微分項を前進差分で，空間微分項を中央差分で離散化せよ」ということでしたね。また陽解法とは，「時間微分項を現在の時間ステップ（ここではnステップ目）で評価せよ」ということでしたね。

まず，(4)式に対して陽解法の関係を組み込みましょう。すると以下のようになります。

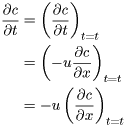(12)

続いて，(12)式中の微分項を離散化します。時間微分項は前進差分で，空間微分項は中央差分で離散化します。

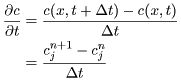(13)

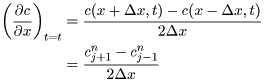(14)

(13)，(14)式を(12)式に代入し，整理すれば，陽解式FTCS差分方程式が以下のように求まります。

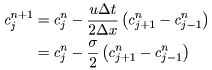(15)

ここに，無次元パラメータσを次のように定義しています。

(16)

　ここで，(15)式を格子図上で表示するとFig.9のようになります。

Fig.9　格子図上での(15)式

Fig.9は，「もし緑色の節点が既知であれば，(15)式を用いて次の時間ステップである赤色の節点が求まる」ということを示しています。