Numerical Solution By Explicit-FTCS Method - 4

■　差分方程式を用いた近似解の計算方法　■

　さて，(4)式に示す移流方程式に対する差分方程式が(15)式のように導かれました。あとは，プログラムを作成するだけですが，その前に，(15)式を用いてどのように近似解が計算されていくのかを少々手計算で追ってみましょう。確認しておきますが，ここで近似解を求めるということは，格子図における節点上での値を求めるということです。

今，解こうとしている移流方程式（問題）とその差分方程式を再度掲載します。

支配方程式（移流方程式）

(4，再載) 解析領域： 初期条件： c(x，0)=0 境界条件： c(0，t)=1

差分方程式（陽解式FTCS差分方程式）

(15，再載) ここに，

�@　解析領域の離散化
　まず，解析領域の離散化を行いましょう。解析領域をx軸方向に分割幅�凅，NX個に分割，またt軸方向に分割幅�冲，NT個に分割します。この条件で分割した格子図をFig.10に示します。

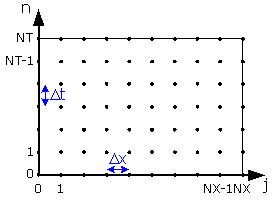Fig.10　格子図

�A　初期条件及び境界条件を格子図に組み込む
　Fig.10に，今分かっている条件を全て書き込んでしまいましょう。分かっている条件とは，初期条件及び境界条件のことです。格子図に組み込むためには，これらも離散化する必要があります。分割幅�凅，�冲に注意してください。初期条件及び境界条件を組み込んだ格子図をFig.11に示します。

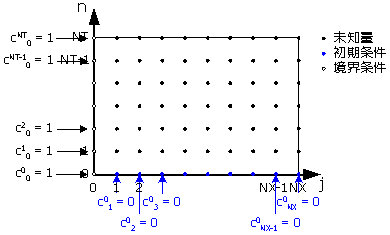Fig.11　初期条件と境界条件

初期条件及び境界条件を組み込むことによって，j=0及びn=0上の節点が既知となりましたね。しかしながら，黒色の節点がまだ未知量のままです。この黒色の節点は，(15)式を用いて求めることが出来ます。

�B−１　未知量の節点を差分方程式により計算する（j=1〜NX-1，n=1上の節点を計算）
　いきなりですが(15)式に，j=1，n=0を代入してみましょう。すると次の式が得られます。

(17)

すると，Fig.12に示すように，未知量であったc¹₁が(17)式によって既知量になります。

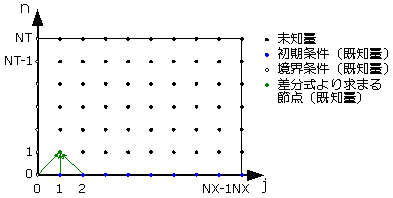Fig.12　差分方程式から未知の節点c11を求める

同様に，(15)式に，j=2〜NX-1，n=0を代入してみましょう。すると次式が得られます。但し，(15)式にはj=0及びj=NXを代入することは出来ません（c⁰_-1，c⁰_NX+1というあり得ない節点がでてきてしまいます）。

	(18a)
	(18b)
	(18c)

(18)式で求めた節点を図示すると，Fig.13のようになります。

Fig.13　差分方程式からn=1における未知の節点を求める

さて，c¹_NXについてですが，(15)式にj=NXが代入できない以上，求めることは出来ません。